题目内容
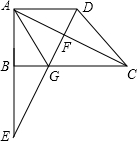
已知：如图，直角梯形ABCD中，AD∥BC，∠ABC=90°，以AB为直径的⊙O切DC边于E点，AD=3cm，BC=5cm．求⊙O的面积．分析：过D作DF垂直于BC，交BC于点F，由AD∥BC，∠ABC=90°，根据两直线平行同旁内角互补可得∠DAB=90°，再由DF与BC垂直得到∠DFB=90°，根据三个角为直角的四边形为矩形可得ABFD为矩形，可得出对边AD=FB，DF=AB，同时得到AD与BC分别为圆O的切线，又CD为圆O的切线，根据切线长定理得到AD=DE，CE=CB，由AD与BC的长，根据CD=DE+EC，等量代换可得出DC的长，再由BC-FB可得出CF的长，在直角三角形CDF中，由DC及CF的长，利用勾股定理求出DF的长，可得出AB的长，进而确定出圆O的半径，利用圆的面积公式即可求出圆O的面积．
解答：
解：过D作DF⊥BC，交BC于点F，
∵AD∥BC，∠ABC=90°，
∴∠DAB=∠ABC=90°，又AB为圆O的直径，
∴AD与圆O相切，BC与圆O相切，又DC与圆O相切，
∴AD=ED，CB=CE，
∵AD=3cm，BC=5cm，
∴CD=DE+EC=AD+BC=3+5=8cm，
又∠DAB=∠BFD=∠ABC=90°，
∴四边形ABFD为矩形，
∴FB=AD=3cm，AB=DF，
∴CF=BC-FB=5-3=2cm，
在Rt△CDF中，DC=8cm，CF=2cm，
根据勾股定理得：DF=
=2
，
∴圆O的直径AB=DF=2
，即半径r=
，
则圆O的面积S=πr2=15πcm2．
解：过D作DF⊥BC，交BC于点F，
∵AD∥BC，∠ABC=90°，
∴∠DAB=∠ABC=90°，又AB为圆O的直径，
∴AD与圆O相切，BC与圆O相切，又DC与圆O相切，
∴AD=ED，CB=CE，
∵AD=3cm，BC=5cm，
∴CD=DE+EC=AD+BC=3+5=8cm，
又∠DAB=∠BFD=∠ABC=90°，
∴四边形ABFD为矩形，
∴FB=AD=3cm，AB=DF，
∴CF=BC-FB=5-3=2cm，
在Rt△CDF中，DC=8cm，CF=2cm，
根据勾股定理得：DF=
| DC2-CF2 |
| 15 |
∴圆O的直径AB=DF=2
| 15 |
| 15 |
则圆O的面积S=πr2=15πcm2．
点评：此题考查了切线的性质，平行线的性质，矩形的性质与判定，切线长定理，以及勾股定理，熟练掌握定理及性质是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
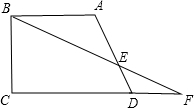已知：如图，直角梯形ABCD中，∠BCD=90°，∠CDA=60°，AB=AD，AB=4，DF=2，求BF的长．
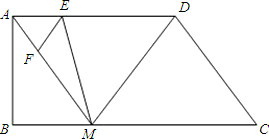、F分别是线段AD、AM上的动点（点E与A、D不重合）且∠FEM=∠AMB，设DE=x，MF=y．
