题目内容
【题目】根据全等多边形的定义,我们把四个角,四条边分别相等的两个凸四边形叫做全等四边形,记作:四边形ABCD≌四边形A1B1C1D1
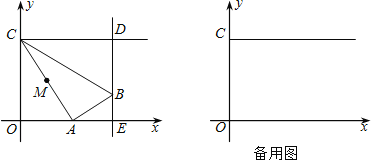
(1)若四边形ABCD≌四边形A1B1C1D1,已知AB3,BC4,ADCD5,B90,D 60,则A1D1 ,B1 , A1C1 (直接写出答案);
(2)如图 1,四边形 ABEF≌四边形CBED,连接AD交 BE于点O,连接F,求证:AOBFOE;
(3)如图 2,若ABA1B1,BCB1C1,CDC1D1,ADA1D1,BB1,求证:四边形ABCD≌四边形A1B1C1D1


【答案】(1)5,90°,210°;(2)见解析;(3)见解析.
【解析】
(1)利用全等四边形的性质即可解决问题.
(2)证明△FEO≌△DEO(SAS)即可解决问题.
(3)如图2中,连接AC,A1C1.利用全等三角形的性质证明四边形的对应角相等即可.
解:(1)∵四边形ABCD≌四边形A1B1C1D1,
∴A1D1=AD=5,∠B1=∠B=90°,∠D=∠D1=60°,∠A=∠A1,∠C=∠C1,
∵∠A+∠C=360°90°60°=210°,
∴∠A1+∠C1=210°,
故答案为:5,90°,210°.
(2)如图1中,
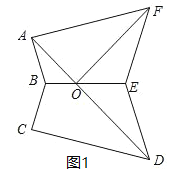
∵四边形ABEF≌四边形CBED,
∴EF=ED,∠FEO=∠DEO,
∵EO=EO,
∴△FEO≌△DEO(SAS),
∴∠FOE=∠DOE,
∵∠AOB=∠DOE,
∴∠AOB=∠FOE;
(3)如图2中,连接AC,A1C1.
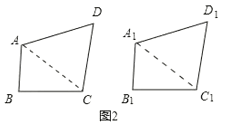
∵AB=A1B1,∠B=∠B1,BC=B1C1,
∴△ABC≌△A1B1C1,
∴AC=A1C1,∠BAC=∠B1A1C1,∠BCA=∠B1C1A1,
∵AD=A1D1,CD=C1D1,
∴△ADC≌△A1D1C1(SSS),
∴∠D=∠D1,∠DAC=∠D1A1C1,∠ACD=∠A1C1D1,
∴∠BAD=∠B1A1D1,∠BCD=∠B1C1D1,
∴四边形ABCD≌四边形A1B1C1D1.

【题目】我校开展的社团活动有:A.动漫社团;B.轮滑社团:C.音乐社团;D.诗歌社团;E.书法社团.学生管理中心为了了解全校500名学生的社团需求,开展了一次调查研究,请将下面的调查过程补全
抽样调查:从七、八、九三个年级中随机抽取男女生各20名进行问卷调研;
收集数据:抽样方法确定后,学生管理中心收集到如下数据(社团项目的编号,用字母代号表示)
B,E,B,A,E,C,C,C,B,B
A,C,E,D,B,A,B,E,C,A
D,D,B,B,C,C,A,A,E,B
C,B,D,C,A,C,C,A,C,E
整理、描述数据:划记、整理、描述样本数据、绘制统计图如下,请补全统计表和统计图
社团项目 | 划记 | 人数 |
A动漫社 |
| 8 |
B轮滑社 | ||
C音乐社 |
| 12 |
D诗歌社 | ||
E书法社 |
| 6 |
合计 | 40 | 40 |
分析数据、推断结论

(1)在扇形统计图中,“B轮滑社团”所在的扇形的圆心角等于 度;
(2)根据学生管理中心获得的样本数据,估计全校大约有 名同学选择D社团.