题目内容
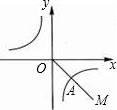
如图,点P是双曲线y=-
(x<0)上一动点,过点P作x轴、y轴的垂线,分别交x轴、y轴于A、B两点,交双曲线y=
于E、F两点.
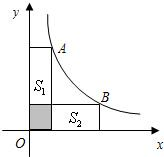
(1)图1中,四边形PEOF的面积S1=______;
(2)图2中,设P点坐标为(-4,3).
①判断EF与AB的位置关系,并证明你的结论;
②记S2=S△PEF-S△OEF,求S2.

| 12 |
| x |
| 6 |
| x |
(1)图1中,四边形PEOF的面积S1=______;
(2)图2中,设P点坐标为(-4,3).
①判断EF与AB的位置关系,并证明你的结论;
②记S2=S△PEF-S△OEF,求S2.

(1)四边形PEOF的面积S1=四边形PAOB的面积+△OAE的面积+△OBF的面积=|k1|+k2=k2+k1=12+6=18
(2)①EF与AB的位置关系为平行,即EF∥AB.
证明:如图,由题意可得:
A(-4,0),B(0,3),E(-4,-
),F(2,3),
∴PA=3,PE=3+
=
,PB=4,PF=4+2=6,
∴
=
=
,
=
=
,
∴
=
,
又∵∠APB=∠EPF,
∴△APB∽△EPF,
∴∠PAB=∠PEF,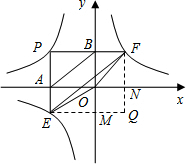
∴EF∥AB;
②S2没有最小值,理由如下:
过E作EM⊥y轴于点M,过F作FN⊥x轴于点N,两线交于点Q,
由上知M(0,-
),N(2,0),Q(2,-
),
而S△EFQ=S△PEF,
则S2=S△PEF-S△OEF=S△EFQ-S△OEF
=S△EOM+S△FON+S矩形OMQN
=12×
+6×
+2×
=6+3+3
=12.
故答案为12.
(2)①EF与AB的位置关系为平行,即EF∥AB.
证明:如图,由题意可得:
A(-4,0),B(0,3),E(-4,-
| 3 |
| 2 |
∴PA=3,PE=3+
| 3 |
| 2 |
| 9 |
| 2 |
∴
| PB |
| PF |
| 4 |
| 6 |
| 2 |
| 3 |
| PA |
| PE |
| 3 | ||
|
| 2 |
| 3 |
∴
| PB |
| PF |
| PA |
| PE |
又∵∠APB=∠EPF,
∴△APB∽△EPF,
∴∠PAB=∠PEF,

∴EF∥AB;
②S2没有最小值,理由如下:
过E作EM⊥y轴于点M,过F作FN⊥x轴于点N,两线交于点Q,
由上知M(0,-
| 3 |
| 2 |
| 3 |
| 2 |
而S△EFQ=S△PEF,
则S2=S△PEF-S△OEF=S△EFQ-S△OEF
=S△EOM+S△FON+S矩形OMQN
=12×
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
=6+3+3
=12.
故答案为12.

练习册系列答案
相关题目