题目内容

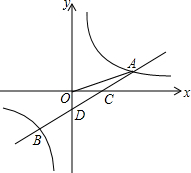
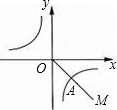
如图，第四象限的角平分线OM与反比例函数y=
k
x
（k≠0）的图象交于点A，已知OA=3
2
，则该函数的解析式为（　　）
A．y=
3
x
B．y=-
3
x
C．y=
9
x
D．y=-
9
x

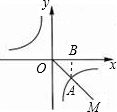
如图，作AB⊥坐标轴．
因为OA是第四象限的角平分线，所以Rt△ABO是等腰直角三角形．
因为OA=3
2
，所以AB=OB=3，
所以A（3，-3）．
再进一步代入y=
k
x
（k≠0），得k=-9．
故选D．
练习册系列答案
相关题目
如图，反比例函数y=
2
x
的图象与一次函数y=kx+b的图象交于点A（m，2），点B（-2，n），一次函数图象与y轴的交点为C．
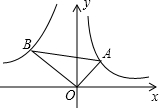
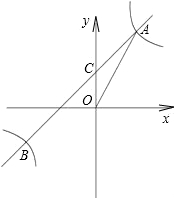（1）求一次函数解析式；
（2）求C点的坐标；
（3）求△AOC的面积．
反比例函数y=
k
x
（k≠0）的图象经过P，如图所示，根据图象可知，反比例函数的解析式为______．
已知y与x的部分取值满足下表：
试猜想y与x的函数关系可能是你们学过的哪类函数，并写出这个函数的解析式．（不要求写x的取值范围）：______．
如图，一次函数y=ax+b的图象与反比例函数y=
k
x
的图象交于A、B两点，与x轴交于点C，与y轴交于点D，已知OA=
10
，tan∠AOC=
1
3
，点B的坐标为（m，-2）．
（1）求反比例函数及一次函数的解析式；
（2）在y轴上存在一点P，使得△PDC与△ODC相似，请你求出P点的坐标．
如图，半圆O的直径AD=12cm，AB，BC，CD分别与半圆O切于点A，E，D．
（1）设AB=x，CD=y，求y与x之间的函数关系式；
（2）如果CD=6，判断四边形ABCD的形状；
（3）如果AB=4，求图中阴影部分的面积．
如图，点P是双曲线y=-
12
x
（x＜0）上一动点，过点P作x轴、y轴的垂线，分别交x轴、y轴于A、B两点，交双曲线y=
6
x
于E、F两点．
（1）图1中，四边形PEOF的面积S1=______；
（2）图2中，设P点坐标为（-4，3）．
①判断EF与AB的位置关系，并证明你的结论；
②记S2=S△PEF-S△OEF，求S2．
如图，已知第一象限内的点A在反比例函数y=
2
x
的图象上，第二象限内的点B在反比例函数y=
k
x
的图象上，且OA⊥OB，cosA=
3
3
，则k的值为（　　）
A．-3B．-4C．-
3
D．-2
3
三角形的面积为12cm2，这时底边上的高ycm底边xcm之间的函数关系用图象表示大致是（　　）
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网