题目内容
【题目】阅读材料,并回答下列问题
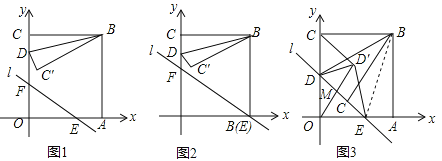
如图1,以AB为轴,把△ABC翻折180°,可以变换到△ABD的位置;
如图2,把△ABC沿射线AC平移,可以变换到△DEF的位置.像这样,其中的一个三角形是另一个三角形经翻折、平移等方法变换成的,这种只改变位置,不改变形状大小的图形变换,叫三角形的全等变换.班里学习小组针对三角形的全等变换进行了探究和讨论
(1)请你写出一种全等变换的方法(除翻折、平移外), .
(2)如图2,前进小组把△ABC沿射线AC平移到△DEF,若平移的距离为2,且AC=5,则DC= .
(3)如图3,圆梦小组展开了探索活动,把△ABC纸片沿DE折叠,使点A落在四边形BCDE内部点A′的位置,且得出一个结论:2∠A′=∠1+∠2.请你对这个结论给出证明.
(4)如图4,奋进小组则提出,如果把△ABC纸片沿DE折叠,使点A落在四边形BCDE外部点A′的位置,此时∠A′与∠1、∠2之间结论还成立吗?若成立,请给出证明,若不成立,写出正确结论并证明.

【答案】(1)旋转;(2)3;(3)见解析;(4)不成立,正确结论:∠2﹣∠1=2∠A',见解析
【解析】
(1)由题意根据三种全等变换翻折、平移、旋转的定义进行判断即可;
(2)根据平移的距离的定义可知AD=2,则DC=AC﹣AD进行求解即可;
(3)根据轴对称及三角形内角和定理进行分析即可得出结论;
(4)由题意根据轴对称及三角形内角和定理,进行分析即可得出结论.
解:(1)除翻折、平移外全等变换的方法还有旋转;
故答案为:旋转.
(2)∵AD=2,AC=5,
∴DC=AC﹣AD=5﹣2=3;
故答案为:3.
(3)∵把△ADE沿DE翻折,得到△A'DE,
∴△ADE≌△A'DE,
∴∠ADE=∠A'DE,∠AED=∠A'ED,
在△DEA'中,∠A'=180°﹣(∠A'DE+∠A'ED);
由平角定义知,∠2=180°﹣∠A'DA=180°﹣2∠A'DE,
∠1=180°﹣∠A'EA=180°﹣2∠A'ED,
∴∠1+∠2=180°﹣2∠A'DE+180°﹣2∠A'ED=2(180°﹣∠A'ED﹣∠A'DE),
∴2∠A′=∠1+∠2.
(4)∠2﹣∠1=2∠A',
理由如下:
∵把△ADE沿DE翻折,得到△A'DE,
∴△ADE≌△A'DE,
∴∠ADE=∠A'DE,∠AED=∠A'ED,
在△DEA'中,∠A'=180°﹣(∠A'DE+∠A'ED),
由平角定义知,∠2=180°﹣∠A'DA=180°﹣2∠A'DE,∠1=2∠A'ED﹣180°,
∴∠2﹣∠1=(180°﹣2∠A'DE)﹣(2∠A'ED﹣180°)=180°-(∠A'DE+∠A'ED),
∴∠2﹣∠1=2∠A'.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案