题目内容
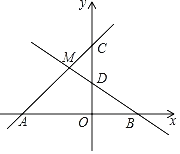
【题目】如图,直线y=x+3分别与x轴、y轴交于点A、C,直线y=mx+![]() 分别与x轴、y轴交于点B、D,直线AC与直线BD相交于点M(﹣1,b)
分别与x轴、y轴交于点B、D,直线AC与直线BD相交于点M(﹣1,b)
(1)不等式x+3≤mx+![]() 的解集为 .
的解集为 .
(2)求直线AC、直线BD与x轴所围成的三角形的面积.
【答案】(1)x≤﹣1;(2)5.
【解析】
(1)直线y=x+3落在直线y=mx+![]() 下方的部分对应的x的取值范围即为所求;
下方的部分对应的x的取值范围即为所求;
(2)先将点M(-1,b)代入y=x+3,求出b,得到M(-1,2),把M(-1,2)代入y=mx+![]() ,求出直线BD的解析式,得到B(2,0).再求出A(-3,0),那么AB=5,然后根据三角形面积公式即可求解.
,求出直线BD的解析式,得到B(2,0).再求出A(-3,0),那么AB=5,然后根据三角形面积公式即可求解.
(1)∵直线y=x+3与直线y=mx+![]() 相交于点M(﹣1,b),
相交于点M(﹣1,b),
∴不等式x+3≤mx+![]() 的解集为x≤﹣1.
的解集为x≤﹣1.
故答案为x≤﹣1;
(2)∵直线y=x+3过点M(﹣1,b),
∴b=﹣1+3=2,M(﹣1,2),
将M(﹣1,2)代入y=mx+![]() ,
,
得2=﹣m+![]() ,解得m=﹣
,解得m=﹣![]() ,
,
∴直线BD的解析式为y=﹣![]() x+
x+![]() ,
,
∴当y=0时,x=2,∴B(2,0).
∵直线AC的解析式为y=x+3,
∴当y=0时,x=﹣3,∴A(﹣3,0).
∴AB=5,
∴S△ABM=![]() ×5×2=5.
×5×2=5.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案
相关题目