ЬтФПФкШн
ЁОЬтФПЁПзлКЯгыЪЕМљЃК
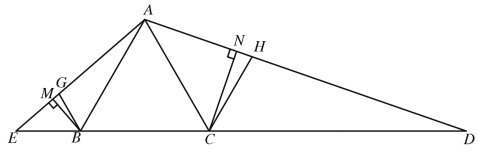
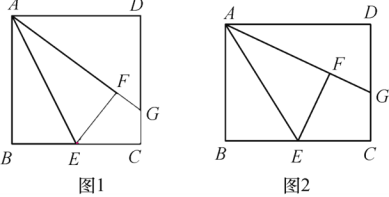
ЮЪЬтЧщОГЃКдкОиаЮABCDжаЃЌЕуEЮЊBCБпЕФжаЕуЃЌНЋЁїABEбижБЯпAEЗелЃЌЪЙЕуBгыЕуFжиКЯЃЌжБЯпAFНЛжБЯпCDгкЕуG.
ЬиР§ЬНОПЁЁЪЕбщаЁзщЕФЭЌбЇЗЂЯжЃК
ЃЈ1ЃЉШчЭМ1ЃЌЕБABЃНBCЪБЃЌAGЃНBCЃЋCGЃЌЧыФужЄУїИУаЁзщЗЂЯжЕФНсТлЃЛ
ЃЈ2ЃЉЕБABЃНBCЃН4ЪБЃЌЧѓCGЕФГЄЃЛ
бгЩьЭиеЙЃКЃЈ3ЃЉЪЕжЊаЁзщЕФЭЌбЇдкЪЕбщаЁзщЕФЦєЗЂЯТЃЌНјвЛВНЬНОПСЫЕБABЁУBCЃН![]() ЁУ2ЪБЃЌЯпЖЮAGЃЌBCЃЌCGжЎМфЕФЪ§СПЙиЯЕЃЌЧыФужБНгаДГіЪЕжЊаЁзщЕФНсТлЃК___________ЃЎ
ЁУ2ЪБЃЌЯпЖЮAGЃЌBCЃЌCGжЎМфЕФЪ§СПЙиЯЕЃЌЧыФужБНгаДГіЪЕжЊаЁзщЕФНсТлЃК___________ЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉ1ЃЛЃЈ3ЃЉAGЃН![]() BCЃЋCG
BCЃЋCG
ЁОНтЮіЁП
ЃЈ1ЃЉШчЭМ1жаЃЌСЌНгEGЃЎжЛвЊжЄУїЁїEGFЁеЁїEGCМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉжЛвЊжЄУїЁїABEЁзЁїECGЃЌМДПЩЭЦГі![]() ЃЌгЩДЫМДПЩНтОіЮЪЬтЃЛ
ЃЌгЩДЫМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉШчЭМ2жаЃЌСЌНгEGЃЎгЩЁїAEBЁеЁїAEFЃЌЁїEGFЁеЁїEGCЃЌЭЦГіAB=AFЃЌBE=EF=ECЃЌFG=GCЃЌгЩABЁУBC=BC=![]() ЁУ2ЃЌЭЦГіAB=
ЁУ2ЃЌЭЦГіAB=![]() BCЃЌПЩЕУAG=AF+FG=AB+CG=
BCЃЌПЩЕУAG=AF+FG=AB+CG=![]() BC+CGЃЎ
BC+CGЃЎ
НтЃК(1)жЄУїЃКСЌНгEG.
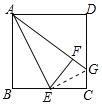
ЁпЁїAEFЪЧгЩЁїAEBЗелЕУЕНЃЌЕуEЮЊBCБпЕФжаЕуЃЌ
ЁрEBЃНEFЃНECЃЌABЃНAFЃЌЁЯAFEЃНЁЯBЃНЁЯCЃН90Ёу.
дкRtЁїEGFКЭRtЁїEGCжаЃЌ![]() ЃЌ
ЃЌ
ЁрRtЁїEGFЁеRtЁїEGC(HL)ЃЎ
ЁрFGЃНGC.
ЁпABЃНAFЃНBCЃЌ
ЁрAGЃНAFЃЋFGЃНBCЃЋCG.
(2)ЁпЁїEGFЁеЁїEGCЃЌ
ЁрЁЯGEFЃНЁЯGEC.
ЁпЁЯAEBЃНЁЯAEFЃЌЁЯBECЃН180ЁуЃЌ
ЁрЁЯAEGЃН90Ёу.
ЁрЁЯAEBЃЋЁЯGECЃН90ЁуЃЌЁЯAEBЃЋЁЯBAEЃН90Ёу.
ЁрЁЯGECЃНЁЯBAE.
ЁпЁЯBЃНЁЯCЃЌ
ЁрЁїABEЁзЁїECG.
Ёр![]()
ЁпECЃН2ЃЌ
ЁрCGЃН1ЃЛ
ЃЈ3ЃЉШчЭМ2жаЃЌСЌНгEGЃЎ
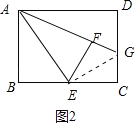
ЁпЁїAEBЁеЁїAEFЃЌЁїEGFЁеЁїEGCЃЌ
ЁрAB=AFЃЌBE=EF=ECЃЌFG=GCЃЌ
ЁпABЃКBC=BC=![]() ЁУ2ЃЌ
ЁУ2ЃЌ
ЁрAB=![]() BCЃЌ
BCЃЌ
ЁрAG=AF+FG=AB+CG=![]() BC+CGЃЎ
BC+CGЃЎ
МДAG=![]() BC+CGЃЎ
BC+CGЃЎ