题目内容
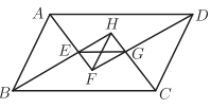
【题目】如图,已知BD平分∠ABC,点F在AB上,点G在AC上,连接FG、FC,FC与BD相交于点H,∠l=∠2.

(1)求证:∠GFH与∠BHC互补;(2)若∠A=75°,FG⊥AC,求∠ACB的度数.
【答案】(1)证明见解析;
(2)∠ACB=75°.
【解析】
(1)根据BD平分∠ABC,∠l=∠2,得出FG∥BD,根据平行线的性质得出∠GFH+∠FHD=180°,等量代换即可得到结论;
(2)根据三角形的内角和和角平分线的定义即可得到结论.
(1)证明:∵BD平分∠ABC,
∴∠2=∠ABD,
∵∠1=∠2,
∴∠1=∠ABD,
∴FG∥BD,
∴∠GFH+∠FHD=180°,
∵∠BHC=∠FHD,
∴∠GFH+∠BHC=180°,
∴∠GFH与∠BHC互补;
(2)∵∠A=75°,FG⊥AC,
∴∠1=90°-75°=15°,
∴∠2=∠1=15°,
∵BD平分∠ABC,
∴∠ABC=30°,
∴∠ACB=180°-∠A-∠ABC=75°.

练习册系列答案
相关题目