题目内容
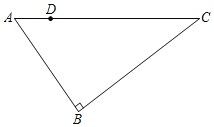
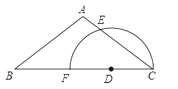
【题目】(1)如图，在
中，
是高，
是角平分线，它们相交于点
，
．求
和
的度数．
(2)一个多边形的内角和是外角和的3倍，它是几边形?若这个多边形的各个内角都相等，求这个多边形的每个内角的度数．
【答案】（1）
=120°，
=10°；（2）多边形为8边形；每个内角的度数为135°．
【解析】
（1）根据三角形的内角和定理，可求出∠BAC的度数，结合
是角平分线，求出∠EAC的度数，由
是高，可以依据直角三角形两锐角互余，可求出∠DAC的度数，代入
中求解；运用角平分线的定义及三角形内角和定理即可求出；
（2）依据多边形内角和公式和外角和为360°，结合已知条件，列出关于边数的方程，解出即可；多边形内角和÷边数即得每个内角的度数.
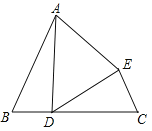
解：（1）
是
的高，
∴
，
∴在
中，
，
在中，
，
∵、
是角平分线，
，
，
∴=40°-30°=10°，
在中，
.
答：=120°，=10°．
（2）设多边形为n边形.
依题意得：（n-2）×180°=3×360°，解之得：n=8，
∴多边形为8边形，
若这个多边形的各个内角都相等，
则每个内角的度数=3×360°÷8=135°．
答：多边形为8边形；每个内角的度数为135°．
练习册系列答案
相关题目
