Question

【题目】已知：如图，∠B＝∠C，BD＝CE，AB＝DC，

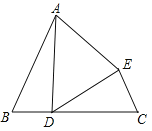
①求证：△ADE为等腰三角形．

②若∠B＝60°，求证：△ADE为等边三角形．

Answer 1

【答案】①见解析；②见解析.

【解析】

①先根据∠B＝∠C，BD＝CE，AB＝DC，判定△ABD≌DCE，得出DA＝DE，进而得到△ADE为等腰三角形；

②根据△ABD≌△DCE，得出∠BAD＝∠CDE，再根据三角形内角和定理和平角的定义，得到∠ADE＝60°，最后可判定等腰△ADE为等边三角形．

①在△ABD和△DCE中，，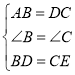

∴△ABD≌△DCE（SAS），

∴DA＝DE，

即△ADE为等腰三角形

②∵△ABD≌△DCE，

∴∠BAD＝∠CDE，

∵∠B＝60°，

∴∠BAD+∠ADB＝120°，

∴∠CDE+∠ADB＝120°，

∴∠ADE＝60°，

又∵△ADE为等腰三角形，

∴△ADE为等边三角形．