题目内容
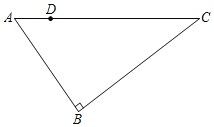
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,点D为AC边上的个动点,点D从点A出发,沿边AC向C运动,当运动到点C时停止,设点D运动时间为t秒,点D运动的速度为每秒1个单位长度的.
(1)当t=2时,求CD的长;
(2)求当t为何值时,线段BD最短?
【答案】(1)8;(2)![]()
【解析】
(1)根据勾股定理即可得到结论;
(2)根据相似三角形的判定和性质定理即可得到结论.
(1)在Rt△ABC中,∠ABC=90°,AB=6,BC=8,
∴AC=![]() =10,
=10,
当t=2时,AD=2,
∴CD=8;
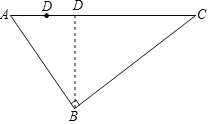
(2)当BD⊥AC时,BD最短,
∵BD⊥AC,
∴∠ADB=∠ABC=90°,
∵∠A=∠A,
∴△ABD∽△ACB,
∴![]() ,即:
,即:![]() ,
,
∴AD=![]() ,
,
∴t=![]() ,
,
∴当t为![]() 时,线段BD最短.
时,线段BD最短.

练习册系列答案
相关题目