题目内容
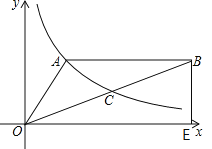
【题目】如图,双曲线y=![]() (x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3),BE⊥x轴,垂足为E.
(x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3),BE⊥x轴,垂足为E.
(1)确定k的值;
(2)若点D(3,m)在双曲线上,求直线AD的解析式;
(3)计算△OAB的面积.
【答案】(1)k=6 (2) y=﹣x+5 (3) 9
【解析】试题分析:(1)将A坐标代入反比例解析式求出k的值即可;
(2)将D坐标代入反比例解析式求出m的值,确定出D坐标,设直线AD解析式为y=kx+b,将A与D坐标代入求出k与b的值,即可确定出直线AD解析式;
(3)过点C作CN⊥y轴,垂足为N,延长BA,交y轴于点M,得到CN与BM平行,进而确定出三角形OCN与三角形OBM相似,根据C为OB的中点,得到相似比为1:2,确定出三角形OCN与三角形OBM面积比为1:4,利用反比例函数k的意义确定出三角形OCN与三角形AOM面积,根据相似三角形面积之比为1:4,求出三角形AOB面积即可.
试题解析:(1)将点A(2,3)代入解析式y=![]() ,
,
得:k=6;
(2)将D(3,m)代入反比例解析式y=![]() ,
,
得:m=![]() =2,
=2,
∴点D坐标为(3,2),
设直线AD解析式为y=kx+b,
将A(2,3)与D(3,2)代入
得: ![]() ,
,
解得: ![]()
则直线AD解析式为y=-x+5;
(3)过点C作CN⊥y轴,垂足为N,延长BA,交y轴于点M,
∵AB∥x轴,
∴BM⊥y轴,
∴MB∥CN,
∴△OCN∽△OBM,
∵C为OB的中点,即![]() ,
,
∴![]() ,
,
∵A,C都在双曲线y=![]() 上,
上,
∴S△OCN=S△AOM=3,
由![]() ,
,
得:S△AOB=9,
则△AOB面积为9.

【题目】已知在线段上依次添加1个点,2个点,3个点,……,原线段上所成线段的总条数如下表:
添加点数 | 1 | 2 | 3 | 4 |
线段总条数 | 3 | 6 | 10 | 15 |
若在原线段上添加n个点,则原线段上所有线段总条数为( )
A. n+2 B. 1+2+3+…+n+n+1 C. n+1 D. ![]()
【题目】某商店计划购进某型号的螺丝、螺母进行销售,有关信息如下表:
原进价(元/个) | 零售价(元/个) | 成套售价(元/套) | |
螺丝 | a | 1.0 | 2.0 |
螺母 | a﹣0.3 | 0.6 | 2.0 |
(1)已知用50元购进螺丝的数量与用20元购进螺母的数量相同,求表中a的值;
(2)若该店购进螺母数量是螺丝数量的3倍还多200个,且两种配件的总量不超过3000个.
①该店计划将一半的螺丝配套(一个螺丝和两个螺母配成一套)销售,其余螺丝、螺母以零售方式销售.请问:怎样进货,才能获得最大利润?最大利润是多少?(用含a的代数式表示)
②由于原材料价格上涨,每个螺丝和螺母的进价都上涨了0.1元.按照①中的最佳进货方案,在销售价不变的情况下,全部售出后,所得利润比①少了260元,请问本次成套的销售量为多少?