Question

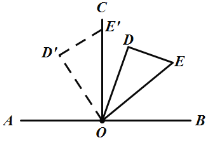
【题目】如图，点O在直线AB上,OC⊥AB .在RtΔODE中，∠ODE=90°，∠DOE=30°，先将ΔODE一边OE与OC重合(如图1)，然后将ΔODE绕点O按顺时针方向旋转(如图2)，当OE与OC 重合时停止旋转.

(1)当∠AOD=80°时，则旋转角∠COE的大小为____________ ;

(2)当OD在OC与OB之间时，求∠AOD∠COE的值;

(3)在ΔODE的旋转过程中，若∠AOE=4∠COD时，求旋转角∠COE的大小.

Answer 1

【答案】（1）20;（2）60°;（3）6°或70°.

【解析】

（1）根据旋转的性质，求出旋转角的度数，即可得到答案；

（2）由旋转的性质可知，，由（1）知，根据角的和差关系，即可得到∠AOD∠COE的值；

（3）根据题意，可分为两种情况进行①OD在OA与OC之间时；②OD在OC与OB之间时；设∠COE为x，根据角的和差关系列出等式，分别求出答案即可.

解：（1）由图1可知，∠AOD=，

如图2，当∠AOD=80°时，有：

∠COE=80°60°=20°，

故答案为：20°.

（2）如图：由（1）知，，

由旋转的性质，可知，

∴；

（3）根据题意，设∠COE为x，则

①如图，当OD在OA与OC之间时，

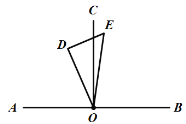
∴∠AOE=90°+x，∠COD=30°，

∵∠AOE=4∠COD，

∴，

解得：；

②如图，当OD在OC与OB之间时，

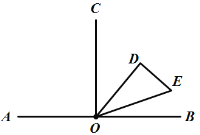
∴∠AOE=90°+x，∠COD=，

∵∠AOE=4∠COD，

∴，

解得：；

∴旋转角∠COE的大小为：6°或70°.