题目内容
当x=2012时,计算(
-
)÷
的结果是( )
| 1 |
| x2-2x |
| 1 |
| x2-4x+4 |
| 2 |
| x2-2x |
分析:把原式括号中的两项的分母分解因式,同时将除式的分母分解因式,然后利用除以一个数等于乘以这个数的倒数把除法运算化为乘法运算,利用乘法分配律化简,约分并通分后,根据同分母分式的减法法则计算,可得出最简结果,然后将x的值代入化简的结果中,即可得到原式的值.
解答:解:(
-
)÷
=[
-
]÷
=[
-
]•
=
•
-
•
=
-
=
=-
,
当x=2012时,原式=-
=-
.
故选A.
| 1 |
| x2-2x |
| 1 |
| x2-4x+4 |
| 2 |
| x2-2x |
=[
| 1 |
| x(x-2) |
| 1 |
| (x-2)2 |
| 2 |
| x(x-2) |
=[
| 1 |
| x(x-2) |
| 1 |
| (x-2)2 |
| x(x-2) |
| 2 |
=
| 1 |
| x(x-2) |
| x(x-2) |
| 2 |
| 1 |
| (x-2)2 |
| x(x-2) |
| 2 |
=
| 1 |
| 2 |
| x |
| 2(x-2) |
=
| x-2-x |
| 2(x-2) |
=-
| 1 |
| x-2 |
当x=2012时,原式=-
| 1 |
| 2012-2 |
| 1 |
| 2010 |
故选A.
点评:此题考查了分式的化简求值,分式的加减运算关键是通分,通分的关键是找出最简公分母;分式的乘除运算关键是约分,约分的关键是找出公因式,有时可以利用运算律来简化运算,若分式中出现多项式,应将多项式分解因式后再计算,此外化简求值题应将原式化为最简后再代值.

练习册系列答案
相关题目
 (2012•瑶海区三模)姚明将带队来我市体育馆进行表演比赛,市体育局在策划本次活动,在与单位协商团购票时推出两种方案.设购买门票数为x(张),总费用为y(元).
(2012•瑶海区三模)姚明将带队来我市体育馆进行表演比赛,市体育局在策划本次活动,在与单位协商团购票时推出两种方案.设购买门票数为x(张),总费用为y(元).
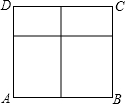 (2012•道里区三模)小张计划用长为6米的铝合金条制成一个矩形窗架(窗架中的横梁、竖梁皆用铝合金条制作)如图所示.若AB的长为x米,窗户的透光面积为S平方米(铝合金条所占的面积忽略不计).
(2012•道里区三模)小张计划用长为6米的铝合金条制成一个矩形窗架(窗架中的横梁、竖梁皆用铝合金条制作)如图所示.若AB的长为x米,窗户的透光面积为S平方米(铝合金条所占的面积忽略不计).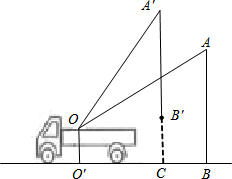 (2012•建阳市模拟)小刘同学在课外活动中观察吊车的工作过程,绘制了如图所示的平面图形.已知吊车吊臂的支点O距离地面的高度OO′=2米.当吊臂顶端由A点抬升至A′点(吊臂长度不变)时,地面B处的重物(大小忽略不计)被吊到B′处,紧绷着的吊绳A′B′=AB.AB垂直地面O′B于点B,A′B′垂直地面O′B于点C,吊臂长度OA′=OA=10米,且cosA=
(2012•建阳市模拟)小刘同学在课外活动中观察吊车的工作过程,绘制了如图所示的平面图形.已知吊车吊臂的支点O距离地面的高度OO′=2米.当吊臂顶端由A点抬升至A′点(吊臂长度不变)时,地面B处的重物(大小忽略不计)被吊到B′处,紧绷着的吊绳A′B′=AB.AB垂直地面O′B于点B,A′B′垂直地面O′B于点C,吊臂长度OA′=OA=10米,且cosA=