题目内容
(2012•河北区三模)用长度一定的不锈钢材料设计成外观为矩形的框架(如图①②③中的一种)(题中的不锈钢材料总长度均指各图中所有黑线的长度和,所有横档和竖档分别与AD、AB平行,材料本身面积忽略不计),设竖档AB=x米,请根据以上图案回答下列问题:

(Ⅰ)在图①中,不锈钢材料总长度为12米,则AD表达式为
(Ⅱ)在图②中,不锈钢材料总长度为12米,则AD表达式为
(Ⅲ)在图③中,如果不锈钢材料总长度为a米,共有n条竖档,写出矩形框架ABCD的面积S与x的函数关系式
x
x;当x为
时,S有最大面积等于
.

(Ⅰ)在图①中,不锈钢材料总长度为12米,则AD表达式为
4-x
4-x
,若矩形框架ABCD的面积为3平方米,则可列方程为x(4-x)=3
x(4-x)=3
.(Ⅱ)在图②中,不锈钢材料总长度为12米,则AD表达式为
4-
x
| 4 |
| 3 |
4-
x
,若矩形框架ABCD的面积为S,请写出S与x的函数关系式| 4 |
| 3 |
S=4x-
x2
| 4 |
| 3 |
S=4x-
x2
.| 4 |
| 3 |
(Ⅲ)在图③中,如果不锈钢材料总长度为a米,共有n条竖档,写出矩形框架ABCD的面积S与x的函数关系式
| a-nx |
| 3 |
| a-nx |
| 3 |
| a |
| 2n |
| a |
| 2n |
| a2 |
| 12n |
| a2 |
| 12n |
分析:(I)由题意可得3AD+3AB=12,从而可得出AD的表达式;根据矩形的面积=长×宽,可得出方程;
(II)由题意可得3AD+4AB=12,从而可得出AD的表达式;根据矩形的面积=长×宽,可得出S与x的函数关系式;
(III)由题意可得3AD+nAB=a,从而可得出AD的表达式,根据矩形的面积=长×宽,可得出S与x的函数关系式,利用配方法可求出S的最大值.
(II)由题意可得3AD+4AB=12,从而可得出AD的表达式;根据矩形的面积=长×宽,可得出S与x的函数关系式;
(III)由题意可得3AD+nAB=a,从而可得出AD的表达式,根据矩形的面积=长×宽,可得出S与x的函数关系式,利用配方法可求出S的最大值.
解答:解:(I)AD=
=4-x,则若矩形框架ABCD的面积为3平方米,则可列方程为:x(4-x)=3;
(II)AD=
=4-
x,
S=x×(4-
x)=4x-
x2;
(III)AD=
,
S=AD×AB=
x=-
x2+
x=-
(x-
)2+
,
当x=
时,S有最大值,最大面积为
.
故答案为:4-x、x(4-x)=3;4-
x、S=4x-
x2;
x、
、
.
| 12-3x |
| 3 |
(II)AD=
| 12-4x |
| 3 |
| 4 |
| 3 |
S=x×(4-
| 4 |
| 3 |
| 4 |
| 3 |
(III)AD=
| a-nx |
| 3 |
S=AD×AB=
| a-nx |
| 3 |
| n |
| 3 |
| a |
| 3 |
| n |
| 3 |
| a |
| 2n |
| a2 |
| 12n |
当x=
| a |
| 2n |
| a2 |
| 12n |
故答案为:4-x、x(4-x)=3;4-
| 4 |
| 3 |
| 4 |
| 3 |
| a-nx |
| 3 |
| a |
| 2n |
| a2 |
| 12n |
点评:本题考查了二次函数的应用,解答本题的关键是得出AD的表达式,根据矩形的面记公式得出函数解析式,注意掌握配方法求最值得应用.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
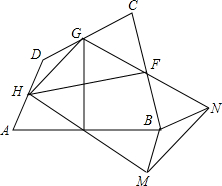 (2012•河北区三模)如图,一任意四边形纸片ABCD中,E,F,G,H为各边中点,则EG与HF的关系为:①相等;②互相垂直;③互相平分;④垂直平分;⑤相等且垂直.请选择正确序号
(2012•河北区三模)如图,一任意四边形纸片ABCD中,E,F,G,H为各边中点,则EG与HF的关系为:①相等;②互相垂直;③互相平分;④垂直平分;⑤相等且垂直.请选择正确序号