题目内容
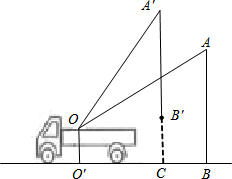 (2012•建阳市模拟)小刘同学在课外活动中观察吊车的工作过程,绘制了如图所示的平面图形.已知吊车吊臂的支点O距离地面的高度OO′=2米.当吊臂顶端由A点抬升至A′点(吊臂长度不变)时,地面B处的重物(大小忽略不计)被吊到B′处,紧绷着的吊绳A′B′=AB.AB垂直地面O′B于点B,A′B′垂直地面O′B于点C,吊臂长度OA′=OA=10米,且cosA=
(2012•建阳市模拟)小刘同学在课外活动中观察吊车的工作过程,绘制了如图所示的平面图形.已知吊车吊臂的支点O距离地面的高度OO′=2米.当吊臂顶端由A点抬升至A′点(吊臂长度不变)时,地面B处的重物(大小忽略不计)被吊到B′处,紧绷着的吊绳A′B′=AB.AB垂直地面O′B于点B,A′B′垂直地面O′B于点C,吊臂长度OA′=OA=10米,且cosA=| 3 |
| 5 |
| 1 |
| 2 |
(1)求此重物在水平方向移动的距离BC;
(2)求此重物在竖直方向移动的距离B′C(精确到0.1米)
分析:(1)首先过点O作OF⊥AB,交A′C于点E,得出OF的长,进而得出OE的长,进而求出BC的长;
(2)首先求出AB,AF的长,进而得出A′E=A′O•cosA′,利用B′C=A′E+EC-A′B′求出即可.
(2)首先求出AB,AF的长,进而得出A′E=A′O•cosA′,利用B′C=A′E+EC-A′B′求出即可.
解答: (1)过点O作OF⊥AB,交A′C于点E,
(1)过点O作OF⊥AB,交A′C于点E,
在Rt△AOF中,cosA=
,OA=10
∴sinA=
,
∴OF=OA•sinA,
=10×
,
=8,
在Rt△A′OE中,OA′=10,sinA′=
,
∴OE=OA′•sinA′,
=10×
,
=5,
∴BC=EF=OF-OE=8-5=3;
(2)在Rt△AOF中,
AF=AO•cosA=10×
=6,
AB=A′B′=6+2=8,
在Rt△A′OE中,sinA′=
,所以cosA′=
,
A′E=A′O•cosA′=10×
,
≈8.66,
B′C=A′E+EC-A′B′=8.66+2-8≈2.7.
答:在水平方向移动3米,在竖直方向移动约2.7米.
 (1)过点O作OF⊥AB,交A′C于点E,
(1)过点O作OF⊥AB,交A′C于点E,在Rt△AOF中,cosA=
| 3 |
| 5 |
∴sinA=
| 4 |
| 5 |
∴OF=OA•sinA,
=10×
| 4 |
| 5 |
=8,
在Rt△A′OE中,OA′=10,sinA′=
| 1 |
| 2 |
∴OE=OA′•sinA′,
=10×
| 1 |
| 2 |
=5,
∴BC=EF=OF-OE=8-5=3;
(2)在Rt△AOF中,
AF=AO•cosA=10×
| 3 |
| 5 |
AB=A′B′=6+2=8,
在Rt△A′OE中,sinA′=
| 1 |
| 2 |
| ||
| 2 |
A′E=A′O•cosA′=10×
| ||
| 2 |
≈8.66,
B′C=A′E+EC-A′B′=8.66+2-8≈2.7.
答:在水平方向移动3米,在竖直方向移动约2.7米.
点评:此题主要考查了解直角三角形的应用,根据已知正确构造直角三角形是解题关键.

练习册系列答案
相关题目

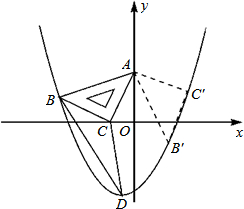 (2012•建阳市模拟)如图,在平面直角坐标系中,将一块腰长为
(2012•建阳市模拟)如图,在平面直角坐标系中,将一块腰长为