题目内容
【题目】如图,在菱形ABCD中,AB=8,点E,F分别在AB,AD上,且AE=AF,过点E作EG∥AD交CD于点G,过点F作FH∥AB交BC于点H,EG与FH交于点O.当四边形AEOF与四边形CGOH的周长之差为12时,AE的值为( ) 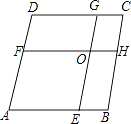
A.6.5
B.6
C.5.5
D.5
【答案】C
【解析】解:∵四边形ABCD是菱形, ∴AD=BC=AB=CD,AD∥BC,AB∥CD,
∵EG∥AD,FH∥AB,
∴四边形AEOF与四边形CGOH是平行四边形,
∴AF=OE,AE=OF,OH=GC,CH=OG,
∵AE=AF,
∴OE=OF=AE=AF,
∵AE=AF,
∴BC﹣BH=CD﹣DG,即OH=HC=CG=OG,
∴四边形AEOF与四边形CGOH是菱形,
∵四边形AEOF与四边形CGOH的周长之差为12,
∴4AE﹣4(8﹣AE)=12,
解得:AE=5.5,
故选C
【考点精析】解答此题的关键在于理解菱形的性质的相关知识,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目