题目内容
【题目】阅读发现:如图①,在△ABC中,∠ACB=2∠B,∠ACB=90°,AD为∠BAC的平分线,且交BC于D,我们发现在AB上截取AE=AC,连结DE,可得AB=AC+CD(不需证明). 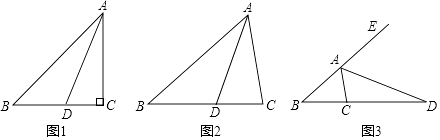
(1)探究:如图②,当∠ACB≠90°时,其他条件不变,线段AB、AC、CD又有怎样的数量关系,写出结果,并证明;
(2)拓展:如图③,当∠ACB=2∠B,∠ACB≠90°时,AD为△ABC的外角∠CAF的平分线,且交BC的延长线于点D,则线段AB、AC、CD又有怎样的数量关系?写出你的猜想,不需证明.
【答案】
(1)解:探究:AB=AC+CD.
证明:如图2,在AB上截取AE=AC,连接ED,
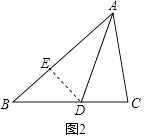
∵AD为∠BAC的角平分线时,
∴∠BAD=∠CAD,
在△AED与△ACD中,
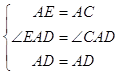 ,
,
∴△AED≌△ACD(SAS),
∴∠AED=∠C,ED=CD,
∵∠ACB=2∠B,
∴∠AED=2∠B,
∵∠AED=∠B+∠EDB,
∴∠B=∠EDB,
∴EB=ED,
∴EB=CD,
∴AB=AE+EB=AC+CD
(2)解:拓展:AB+AC=CD.
理由:如图3,在BA的延长线上截取AE=AC,连接ED.
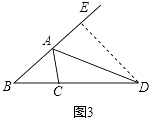
∵AD平分∠FAC,
∴∠EAD=∠CAD,
在△AED与△ACD中,
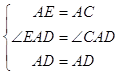 ,
,
∴△AED≌△ACD(SAS),
∴ED=CD,∠AED=∠ACD,
∴∠FED=∠ACB,
又∵∠ACB=2∠B,
∴∠FED=2∠B,
又∵∠FED=∠B+∠EDB,
∴∠EDB=∠B,
∴EB=ED,
∴EA+AB=EB=ED=CD,
∴AC+AB=CD.
【解析】(1)探究:在AB上截取AE=AC,连接ED,由AD为∠BAC的角平分线时,得到∠BAD=∠CAD,通过△AED≌△ACD得到∠AED=∠C,ED=CD,由已知得到∠B=∠EDB,根据等腰三角形的性质得到EB=ED,即可得解;(2)拓展:在BA的延长线上截取AE=AC,连接ED,由AD为∠BAC的角平分线时,得到∠BAD=∠CAD,通过△AED≌△ACD得到∠AED=∠C,ED=CD,由已知得到∠B=∠EDB,根据等腰三角形的性质得到EB=ED,即可得解.
【考点精析】根据题目的已知条件,利用等腰直角三角形和角的平分线的相关知识可以得到问题的答案,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案