Question

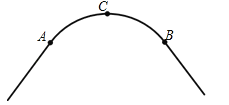
【题目】如图，一条公路的转弯处是一段圆弧（）．

（1）用直尺和圆规作出所在圆的圆心O；（要求保留作图痕迹，不写作法）

（2）若的中点C到弦AB的距离为20m，AB=80m，求所在圆的半径．

Answer 1

【答案】（1）作图见试题解析；（2）50m．

【解析】

试题分析：（1）连结AC、BC，分别作AC和BC的垂直平分线，两垂直平分线的交点为点O，如图1；

（2）连接OA，OC，OC交AB于D，如图2，由C为的中点，得到OC⊥AB，AD=BD=AB=40，则CD=20，设⊙O的半径为r，在Rt△OAD中利用勾股定理得到r的值．

试题解析：（1）如图1，点O为所求；

（2）连接OA，OC，OC交AB于D，如图2，∵C为的中点，∴OC⊥AB，∴AD=BD=AB=40，设⊙O的半径为r，则OA=r，OD=OD﹣CD=r﹣20，在Rt△OAD中，∵，∴，解得r=50，即所在圆的半径是50m．