题目内容
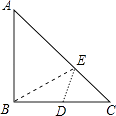
【题目】已知:如图,∠A=∠ADE,∠C=∠E.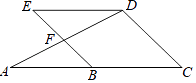
(1)若∠EDC=3∠C,求∠C的度数.
(2)求证:BE∥CD.
【答案】
(1)解:∵∠A=∠ADE,
∴AC∥DE,
∴∠EDC+∠C=180°,
又∵∠EDC=3∠C,
∴4∠C=180°,即∠C=45°;
(2)证明:∵AC∥DE,
∴∠E=∠ABE,
又∵∠C=∠E,
∴∠C=∠ABE,
∴BE∥CD.
【解析】(1)首先依据内错角线段两直线平行可证明AC∥DE,然后根据两直线平行,同旁内角互补,即可得出∠C+∠EDC=180°,结合条件∠EDC=3∠C可求得∠C的度数;
(2)根据AC∥DE,∠C=∠E,通过等量代换可得出∠C=∠ABE,最后依据平行线的判定定理进行证明即可.
【考点精析】通过灵活运用平行线的判定,掌握同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行即可以解答此题.

练习册系列答案
相关题目