题目内容
【题目】完成下面的证明．
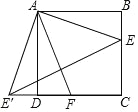
已知，如图所示，BCE，AFE是直线，
AB∥CD，∠1=∠2，∠3=∠4．
求证：AD∥BE
证明：∵ AB∥CD （已知）
∴ ∠4 =∠ （ ）
∵ ∠3 =∠4 （已知）
∴ ∠3 =∠ （ ）
∵ ∠1 =∠2 （已知）
∴ ∠1+∠CAF =∠2+ ∠CAF ( )
即：∠ =∠ ．
∴ ∠3 =∠ （ ）
∴ AD∥BE （ ）
【答案】详见解析.
【解析】试题分析：由AB∥DC，利用两直线平行，同位角角相等得到一对角相等，再由已知角相等，利用等量代换得到∠3=∠BAE，根据∠1=∠2，利用等式的性质得到∠BAE=∠CAD，等量代换得到一对内错角相等，利用内错角相等，两直线平行即可得证．
证明：∵AB∥DC（已知），
∴∠4=∠BAE（两直线平行，同位角相等），
∵∠3=∠4（已知），
∴∠3=∠BAE（等量代换），
∵∠1=∠2（已知），
∴∠1+∠CAE=∠2+∠CAE（等式性质），
即∠BAE=∠CAD，
∴∠3=∠CAD（等量代换），
∴AB∥CD（ 内错角相等，两直线平行）．
练习册系列答案
阅读快车系列答案
相关题目
