题目内容
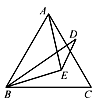
【题目】如图,已知,在△ABC中,∠B<∠C,AD平分∠BAC,E是线段AD(除去端点A、D)上一动点,EF⊥BC于点F.
(1)若∠B=40°,∠DEF=10°,求∠C的度数.
(2)当E在AD上移动时,∠B、∠C、∠DEF之间存在怎样的等量关系?请写出这个等量关系,并说明理由.
【答案】
(1)解:∵EF⊥BC,∠DEF=10°,
∴∠EDF=80°.
∵∠B=40°,
∴∠BAD=∠EDF-∠B=80°-40°=40°.
∵AD平分∠BAC,∴∠BAC=80°.
∴∠C=180°-40°-80°=60°.
(2)解:∠C-∠B=2∠DEF.理由如下:
∵EF⊥BC,∴∠EDF=90°-∠DEF.
∵∠EDF=∠B+∠BAD,
∴∠BAD=90°-∠DEF-∠B.
∵AD平分∠BAC,
∴∠BAC=2∠BAD=180°-2∠DEF-2∠B.
∴∠B+180°-2∠DEF-2∠B+∠C=180°.
∴∠C-∠B=2∠DEF.
【解析】 (1)根据垂直的定义及三角形的内角和得出∠EDF=80°. 根据三角形的外角性质得出∠BAD=∠EDF-∠B=80°-40°=40°.根据角平分线的定义得出∠BAC=80°.根据三角形的内角和得出∠C的度数 ;
(2)∠C-∠B=2∠DEF.理由如下:根据三角形的内角和及外角的性质得出∠BAD=90°-∠DEF-∠B.根据角平分线的定义得出∠BAC=2∠BAD=180°-2∠DEF-2∠B ,根据三角形的内角和得出∠B+180°-2∠DEF-2∠B+∠C=180°.从而得出结论;∠C-∠B=2∠DEF .

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目