题目内容
【题目】如图,在正方形ABCD中,点E,F分别在BC,CD上,且∠EAF=45°,将△ABE绕点A顺时针旋转90°,使点E落在点E'处,则下列判断不正确的是( )
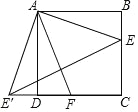
A.△AEE′是等腰直角三角形 B.AF垂直平分EE'
C.△E′EC∽△AFD D.△AE′F是等腰三角形
【答案】D.
【解析】
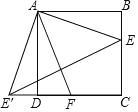
试题分析:因为将△ABE绕点A顺时针旋转90°,使点E落在点E'处,
∴AE′=AE,∠E′AE=90°,∴△AEE′是等腰直角三角形,故A正确;
∵将△ABE绕点A顺时针旋转90°,使点E落在点E'处,∴∠E′AD=∠BAE,
∵四边形ABCD是正方形,∴∠DAB=90°,∵∠EAF=45°,∴∠BAE+∠DAF=45°,
∴∠E′AD+∠FAD=45°,∴∠E′AF=∠EAF,∵AE′=AE,∴AF垂直平分EE',故B正确;
∵AF⊥E′E,∠ADF=90°,∴∠FE′E+∠AFD=∠AFD+∠DAF,∴∠FE′E=∠DAF,
∴△E′EC∽△AFD,故C正确;∵AD⊥E′F,但∠E′AD不一定等于∠DAE′,
∴△AE′F不一定是等腰三角形,故D错误;
故选D.

练习册系列答案
相关题目
