题目内容
【题目】如图，经过原点的抛物线y=﹣x2+2mx（m＞0）与x轴的另一个交点为A．过点P（1，m）作直线PM⊥x轴于点M，交抛物线于点B．记点B关于抛物线对称轴的对称点为C（B、C不重合）．连接CB，CP．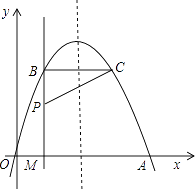
（1）当m=3时，求点A的坐标及BC的长；
（2）当m＞1时，连接CA，问m为何值时CA⊥CP？
（3）过点P作PE⊥PC且PE=PC，问是否存在m，使得点E落在坐标轴上？若存在，求出所有满足要求的m的值，并定出相对应的点E坐标；若不存在，请说明理由．
【答案】
（1）解：当m=3时，y=﹣x2+6x
令y=0得﹣x2+6x=0
∴x1=0，x2=6，
∴A（6，0）
当x=1时，y=5
∴B（1，5）
∵抛物线y=﹣x2+6x的对称轴为直线x=3
又∵B，C关于对称轴对称
∴BC=4．
（2）解：连接AC，过点C作CH⊥x轴于点H（如图1）
由已知得∠ACP=∠BCH=90°
∴∠ACH=∠PCB
又∵∠AHC=∠PBC=90°
∴△ACH∽△PCB，
∴ 
，
∵抛物线y=﹣x2+2mx的对称轴为直线x=m，其中m＞1，
又∵B，C关于对称轴对称，
∴BC=2（m﹣1），
∵B（1，2m﹣1），P（1，m），
∴BP=m﹣1，
又∵A（2m，0），C（2m﹣1，2m﹣1），
∴H（2m﹣1，0），
∴AH=1，CH=2m﹣1，
∴ 
，
∴m= 
．
（3）解：∵B，C不重合，∴m≠1，
（I）当m＞1时，BC=2（m﹣1），PM=m，BP=m﹣1，
（i）若点E在x轴上（如图1），
∵∠CPE=90°，
∴∠MPE+∠BPC=∠MPE+∠MEP=90°，PC=EP，
在△BPC和△MEP中，
，
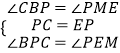∴△BPC≌△MEP，
∴BC=PM，
∴2（m﹣1）=m，
∴m=2，此时点E的坐标是（2，0）；
（ii）若点E在y轴上（如图2），
过点P作PN⊥y轴于点N，
易证△BPC≌△NPE，
∴BP=NP=OM=1，
∴m﹣1=1，
∴m=2，
此时点E的坐标是（0，4）；
（II）当0＜m＜1时，BC=2（1﹣m），PM=m，BP=1﹣m，
（i）若点E在x轴上（如图3），
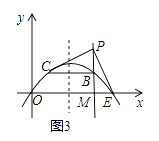
易证△BPC≌△MEP，
∴BC=PM，
∴2（1﹣m）=m，
∴m= 
，此时点E的坐标是（ 
，0）；
（ii）若点E在y轴上（如图4），
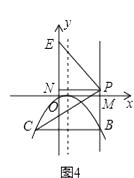
过点P作PN⊥y轴于点N，
易证△BPC≌△NPE，
∴BP=NP=OM=1，
∴1﹣m=1，∴m=0（舍去），
综上所述，当m=2时，点E的坐标是（2，0）或（0，4），
当m= 时，点E的坐标是（ ，0）．
【解析】（1）利用中点公式可知，两对称点的横坐标和的一半就是对称轴的横坐标坐标；（2）由垂直可构造出相似三角形，用m的代数式表示相似三角形的边长，代入比例式中构建方程，即可求出；（3）须分类讨论，m＞1或0＜m＜1，再分点E在x轴上或y 轴上，由垂直和相等关系构建全等三角形，对应边相等可求出.
