Question

【题目】如图，某电信部门计划修建一条连接B，C两地的电缆．测量人员在山脚A点测得B，C两地的仰角分别为30°、45°，在B地测得C地的仰角为60°．已知C地比A地高200m，电缆BC至少长多少米（精确到1m）？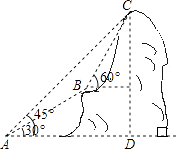

Answer 1

【答案】解：过B点分别作BE⊥CD、BF⊥AD，垂足分别为E、F．

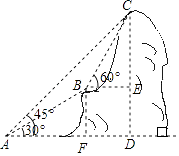
设BC=xm．

∵∠CBE=60°，

∴BE= x，CE= x．

∵CD=200，

∴DE=200﹣ x．

∴BF=DE=200﹣ x，DF=BE= x．

∵∠CAD=45°，

∴AD=CD=200．

∴AF=200﹣ x．

在Rt△ABF中，tan30°= = ，

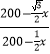解得，x=200（ ﹣1）≈147m，

答：电缆BC至少长147米．

【解析】须通过作垂线把特殊角放到直角三角形中，利用三角函数构建方程，求出未知量.