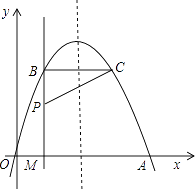��Ŀ����
����Ŀ����ͬһƽ���ڵ�ͼ��M��N���������¶��壺PΪͼ��M������һ�㣬QΪͼ��N������һ�㣬���P��Q�����ľ�������Сֵ����ô�������СֵΪͼ��M��N��ġ��վ��롰������d��M��N����
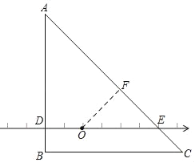
��ͼ������ֱ��������ABC��һ��ֱ�DZ�AB��ֱ�����ڵ�D��б��AC�����ύ�ڵ�E�������ϵ�O��ʾ����������0����AB��BC��8��AD��6��OD��2����O����BC�ľ������߶�DB�ij���ȣ�
��1����d����O����E����
��2����d����O����ABC����
���𰸡���1��4����2��2.
��������
��1�����ݵ���ֱ�������ε����ʺ��߶εĺͲ��ϵ���OE��4���ٸ������վ������Ķ���ɵ�d����O����E����4��
��2������O��OF��AC�ڵ�F���ɵ�OF��FE����OF��FE��x����Rt��OEF�У������O����AC����OF��2![]() ����һ���õ�������ABC����������һ��Q��O��Q�����ľ������СֵΪ2���ٸ������վ������Ķ���ɵ�d����O����ABC����2��
����һ���õ�������ABC����������һ��Q��O��Q�����ľ������СֵΪ2���ٸ������վ������Ķ���ɵ�d����O����ABC����2��
�⣺��1���ߵ���ֱ��������ABC��AB��BC��8��
���C����A��45��
��ABC��90����
��AB��ֱ�����ڵ�D��
���ADE����ABC��90����
��BC��DE
���AED����C����A��45����
��AD��DE��
��AD��6��
��DE��AD��6��
��OD��2��
��OE��4��
��d����O����E����4��
��2������O��OF��AC�ڵ�F��
�ߡ�AED��45����OE��4��
���AED����FOE��45��
��OF��FE��
��OF��FE��x��
��Rt��OEF�У�x2+x2��16x2��8��![]() ����ֵ��ȥ����
����ֵ��ȥ����
![]() ��
��
���O����AC����OF��![]() ��
��
��AB��8��AD��6��
��DB��AB��AD��2��
�ߵ�O����BC�ľ������߶�DB�ij���ȣ�
���O����BC������2��
�ߵ�O����AB����OD��2��
�������ABC����������һ��Q��O��Q�����ľ������СֵΪ2��
��d����O����ABC����2��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��ij������������ÿ̨���۷ֱ�Ϊ2000Ԫ��1700Ԫ��A��B�����ͺŵĿյ�������ǽ����ܵ����������
����ʱ�� | �������� | �������� | |
A���ͺ� | B���ͺ� | ||
��һ�� | 3̨ | 5̨ | 18000Ԫ |
�ڶ��� | 4̨ | 10̨ | 31000Ԫ |
�����ۡ��ۼ۾����ֲ��䣬������������������ɱ���
��1����A��B�����ͺŵĿյ������۵��ۣ�
��2�����������ò�����54000Ԫ�Ľ���ٲɹ��������ͺŵĿյ���30̨����A���ͺŵĿյ�����ܲɹ�����̨��
����Ŀ��ijˮ���̵꾭��һ��ƻ��������20����ÿ��25ǧ��Ϊ�������������ǧ�����ֱ���������������ʾ����¼�����
��������IJ�ֵ����λ��ǧ�ˣ� | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
���� | 1 | 4 | 2 | 3 | 2 | 8 |
��1����20��ƻ���У����ص�һ��������һ����ض���ǧ�ˣ�
��2����������Ƚϣ���20��ƻ���ܼƳ����������ǧ�ˣ�
��3����ƻ��ÿǧ���ۼ�![]() Ԫ���������20��ƻ����������Ԫ��
Ԫ���������20��ƻ����������Ԫ��