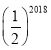题目内容
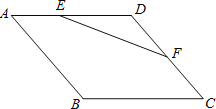
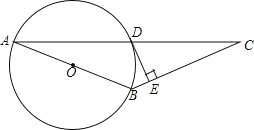
【题目】已知:如图,AB为⊙O的直径,⊙O过AC的中点D,DE⊥BC于点E.
(1)求证:DE为⊙O的切线;
(2)若DE=2,tanC=![]() ,求⊙O的直径.
,求⊙O的直径.
【答案】(1)证明见解析;(2)5.
【解析】(1)连接OD,利用D是AC中点,O是AB中点,那么OD就是△ABC的中位线,利用三角形中位线定理,可知OD∥BC,而DE⊥BC,则∠DEC=90°,利用平行线的性质,有∠ODE=∠DEC=90°,即DE是⊙O的切线;
(2)连接BD,由于AB是直径,那么∠ADB=90°,即BD⊥AC,在△ABC中,点D是AC中点,于是BD是AC的垂直平分线,那么BA=BC,在Rt△CDE中,DE=2,tanC=![]() ,可求CE=4,再利用勾股定理可求CD=2
,可求CE=4,再利用勾股定理可求CD=2![]() ,同理在Rt△CDB中,CD=2
,同理在Rt△CDB中,CD=2![]() ,tanC=
,tanC=![]() ,可求BD=
,可求BD=![]() ,利用勾股定理可求BC=5,从而可知BA=BC=5.
,利用勾股定理可求BC=5,从而可知BA=BC=5.
(1)证明:连接OD.
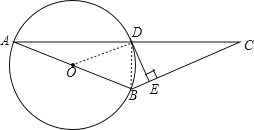
∵D为AC中点,O为AB中点,
∴OD为△ABC的中位线,
∴OD∥BC,
∵DE⊥BC,
∴∠DEC=90°,
∴∠ODE=∠DEC=90°,
∴OD⊥DE于点D,
∴DE为⊙O的切线;
(2)连接DB,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴DB⊥AC,
∴∠CDB=90°
∵D为AC中点,
∴AB=BC,
在Rt△DEC中,
∵DE=2,tanC=![]() ,
,
∴EC=![]() =4,
=4,
由勾股定理得:DC=2![]() ,
,
在Rt△DCB中,BD=DCtanC=![]() ,
,
由勾股定理得:BC=5,
∴AB=BC=5,
∴⊙O的直径为5.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案【题目】某儿童游乐园门票价格规定如下表:
购票张数 | 1~50张 | 51~100张 | 100张以上 |
每张票的价格 | 13元 | 11元 | 9元 |
某校七年级(1)、(2)两个班共102人今年6.1儿童节去游该游乐园,其中(1)班人数较少,不足50人.经估算,如果两个班都以班为单位购票,则一共应付1218元.问:
(1)两个班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可以节省多少钱?
(3)如果七年级(1)班有10名学生因学校有任务不能参加这次旅游,请你为两个班设计出购买门票的方案,并指出最省钱的方案.
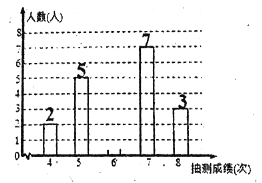
【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值 (单位:克) |
|
| 0 | 1 | 3 | 6 |
袋 数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)这批样品的平均质量比标准质量多还是少?多或少几克?
(2)若标准质量为450克,则抽样检测的20袋食品的总质量为多少克?
(3)若该种食品的合格标准为450±5克,求该食品的抽样检测的合格率.