题目内容
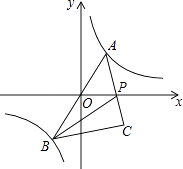
【题目】在平面直角坐标系中，O为坐标原点，设点P（1，t）在反比例函数y= 
的图象上，过点P作直线l与x轴平行，点Q在直线l上，满足QP=OP．若反比例函数y= 
的图象经过点Q，则k= ．
【答案】2+2 
或2﹣2
【解析】解：∵点P（1，t）在反比例函数y= 
的图象上， ∴t= 
=2，
∴P（1.2），
∴OP= 
= ，
∵过点P作直线l与x轴平行，点Q在直线l上，满足QP=OP．
∴Q（1+ ，2）或（1﹣ ，2）
∵反比例函数y= 
的图象经过点Q，
∴2= 
或2= 
，解得k=2+2 或2﹣2
故答案为2+2 或2﹣2 ．
把P点代入y= 求得P的坐标，进而求得OP的长，即可求得Q的坐标，从而求得k的值．
练习册系列答案
相关题目
