题目内容
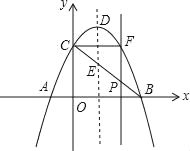
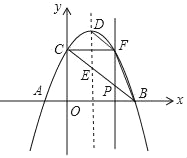
【题目】如图,抛物线y=﹣x2+2x+3与x轴交于A,B两点(点A在点B的左侧),与y轴相交于点C,顶点为D,连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点(P不与B,C两点重合),过点P作x轴的垂线交抛物线于点F,设点P的横坐标为m(0<m<3)
(1)当m为何值时,四边形PEDF为平行四边形;
(2)设△BCF的面积为S,求S的最大值.
【答案】(1)m=2(2)![]()
【解析】试题分析:(1)PF的长就是当x=m时,抛物线的值与直线BC所在一次函数的值的差.可先根据B,C的坐标求出BC所在直线的解析式,然后将m分别代入直线BC和抛物线的解析式中,求得出两函数的值的差就是PF的长. 根据直线BC的解析式,可得出E点的坐标,根据抛物线的解析式可求出D点的坐标,然后根据坐标系中两点的距离公式,可求出DE的长,然后让PF=DE,即可求出此时m的值.
(2)可将△BCF分成两部分来求:一部分是△PFC,以PF为底边,以P的横坐标为高即可得出△PFC的面积. 一部分是△PFB,以PF为底边,以P、B两点的横坐标差的绝对值为高,即可求出△PFB的面积. 然后根据△BCF的面积=△PFC的面积+△PFB的面积,可求出关于S、m的函数关系式.
解:(1)对于抛物线y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点D(1,4)
令x=0,得到y=3;
令y=0,得到﹣x2+2x+3=0,即(x﹣3)(x+1)=0,
解得:x=﹣1或x=3,
则A(﹣1,0),B(3,0),C(0,3),抛物线对称轴为直线x=1;
设直线BC的函数解析式为y=kx+b,
把B(3,0),C(0,3)分别代入得:![]() ,
,
解得:k=﹣1,b=3,
∴直线BC的解析式为y=﹣x+3,
当x=1时,y=﹣1+3=2,
∴E(1,2),
∴DE=4﹣2=2,
∵PF⊥x轴,
∴P(m,﹣m+3),F(m,﹣m2+2m+3),
∴线段PF=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m,
连接DF,由PF∥DE,得到当PF=DE时,四边形PEDF为平行四边形,
由﹣m2+3m=2,得到m=2或m=1(不合题意,舍去),
当m=2时,四边形PEDF为平行四边形;
(2)∵B(3,0),
∴OB=3,
∴S=![]() PFOB=
PFOB=![]() ×3(﹣m2+3m)=﹣
×3(﹣m2+3m)=﹣![]() (m﹣
(m﹣![]() )2+
)2+![]() (0<m<3),
(0<m<3),
则当m=![]() 时,S取得最大值为
时,S取得最大值为![]() .
.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案