��Ŀ����
����Ŀ����ͼ����һ��������ԭ��O�͵�B������һ�£��õ�һ����������������ͼ�е�A��ʾ-10����B��ʾ10����C��ʾ18�����dzƵ�A�͵�C�����������28�����ȵ�λ������P�ӵ�A��������2��λ/����ٶ��������������������������˶����ӵ�O�˶�����B�ڼ��ٶȱ�Ϊԭ����һ�룬֮�����ָ̻�ԭ�٣�ͬʱ������Q�ӵ�C��������1��λ/����ٶ���������ĸ������˶����ӵ�B�˶�����O�ڼ��ٶȱ�Ϊԭ����������֮��Ҳ���ָ̻�ԭ�٣����˶���ʱ��Ϊt�룬�ʣ�
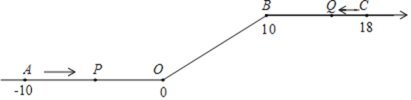
��1������P�ӵ�A�˶�����C��Ҫ________�룻
��2��P��Q��������ʱ�����������M����Ӧ�����Ƕ��٣�
��3����tΪ��ֵʱ��P��O���������������ij�����Q��B���������������ij������.
���𰸡���1��19�룻��2��������M����Ӧ������![]() ����3��t��ֵΪ2��6.5��11��17
����3��t��ֵΪ2��6.5��11��17
��������
��1������·�̳����ٶȵ���ʱ�䣬�ɵô𰸣�
��2����������ʱP��Q�˶���ʱ����ȣ��ɵ÷��̣��ⷽ�̣��ɵô𰸣�
��3������PO��BQ��ȣ��ɵ÷��̣��ⷽ�̣��ɵô𰸣�
�⣺��1����P�˶�����Cʱ������ʱ��t=![]() ���룩��
���룩��
��2�������֪��P��Q�����������߶�OB����M������OM=![]() ��
��
��![]() ��
��
���![]() ����������M����Ӧ������
����������M����Ӧ������![]() ��
��
��3��P��O���������������ij�����Q��B���������������ij��������4�ֿ��ܣ�
�ٶ���Q��CB�ϣ�����P��AO�ϣ���8-t=10-2t����ã�t=2��
�ڶ���Q��CB�ϣ�����P��OB�ϣ���8-t=��t-5����1����ã�t=6.5��
�۶���Q��BO�ϣ�����P��OB�ϣ���2��t-8��=��t-5����1����ã�t=11��
�ܶ���Q��OA�ϣ�����P��BC�ϣ���10+2��t-15��=t-13+10����ã�t=17��
����������t��ֵΪ2��6.5��11��17��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ����֪a��b��c���㣺 (1)5(a+3)+2|b2|=0�� (2)![]() x
x![]() y
y![]() +2a
+2a![]() b+c+1���ߴζ���ʽ��
b+c+1���ߴζ���ʽ��
�����ʽab[ab(2abcac3ab)4ac]abc��ֵ..
����Ŀ��������ʮһ���ƽ����ڼ�,ij�羰����7�������ÿ�����ε������仯���±�(������ʾ��ǰһ��������,������ʾ��ǰһ���ٵ�����,��λ:����),��֪9��30�յ��ο�����Ϊ0.3����,��ش���������:
�� �� | 1�� | 2�� | 3�� | 4�� | 5�� | 6�� | 7�� |
�����仯 | +1.8 | +0.8 | +0.2 | -0.4 | -0.8 | +0.2 | -1.0 |
(1)�������ο����������� ��,���ٵ��� �գ�
(2)����9��30�յ��ο�����Ϊ0��,������ͳ��ͼ��ʾ��7����ο������仯���?
(3)����7����ο������Ƕ�������.