题目内容
【题目】如图，△ABC中，∠C=70°，⊙O切CA、CB分别于点A和点B，则弦AB所对的圆周角的度数为（ ）
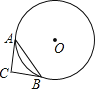
A. 110° B. 55° C. 55°或 110° D. 55 或 125°
【答案】D
【解析】
由CA、CB是⊙O的切线，∠C=70°，根据切线的性质，易求得∠AOB的度数，然后由圆周角定理，可求得当点D在优弧AB上时，∠ADB的值，由圆的内接四边形的性质，可求得当点E在劣弧AB上时，∠AEB的度数，继而求得答案．
连接OA、OB，
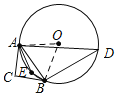
∵CA、CB是⊙O的切线，
∴OA⊥CA，OB⊥CB，
∴∠CAO=∠CBO=90°，
∵∠C=70°，
∴∠AOB=360°-∠CAO-∠CBO-∠C=110°，
∴当点D在优弧AB上时，∠ADB=
∠AOB=55°；
当点E在劣弧AB上时，∠AEB=180°-∠ADB=125°．
∴弦AB所对的圆周角的度数是：55°或125°．
故选D．
练习册系列答案
相关题目
