题目内容
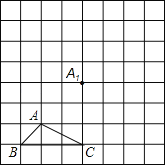
【题目】如图,两个等腰直角三角形△ABC和△CDE中,∠ACB=∠DCE=90°,AB=13![]() ,CD=5
,CD=5![]() ,△CDE绕点C在平面内自由旋转,当A、E、D三点共线时,AD的长是______.
,△CDE绕点C在平面内自由旋转,当A、E、D三点共线时,AD的长是______.

【答案】7或17
【解析】
分两种情况:①当射线AD在直线AC的上方时,作CH⊥AD于点H,根据等腰直角三角形的性质和勾股定理,可得CH、AH的长,②当射线AD在直线AC的下方时,作CH⊥AD于点H,同理可得CH、AH的长,进而即可求解.
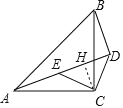
①当射线AD在直线AC的上方时,作CH⊥AD于点H,
∵CE=CD,∠ECD=90°,CH⊥DE,CD=5![]() ,
,
∴DE=5![]() ×
×![]() =10,
=10,
∴EH=DH=CH=![]() DE=5,
DE=5,
∵CA=CB,∠ACB=90°,AB=13![]() ,
,
∴AC=13![]() ÷
÷![]() =13,
=13,
∴在Rt△ACH中,AH=![]() ,
,
∴AD=AH+DH=12+5=17;
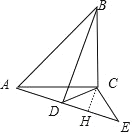
②当射线AD在直线AC的下方时,作CH⊥AD于点H,
同理可得:CH=5,AH=12,
∴AD=AHDH=125=7.
综上所述, AD的值为17或7.
故答案是:7或17.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目