题目内容
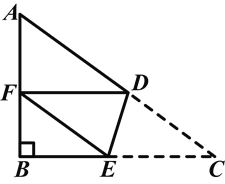
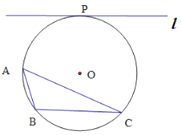
【题目】已知⊙O为△ABC的外接圆,直线l与⊙O相切于点P,且![]() ∥BC.
∥BC.
(1) 连接PO,并延长交⊙O于点D,连接AD.证明: AD平分∠BAC;
(2) 在(1)的条件下,AD交BC于点E,连接CD.若DE=2,AE=6.试求CD的长.
【答案】(1)证明见解析;(2)CD=4.
【解析】试题分析:(1)由切线的性质得到PD⊥l,再由![]() ∥BC,得到PD垂直平分弦BC,由垂径定理得到弧BD=弧DC,即可得到结论;
∥BC,得到PD垂直平分弦BC,由垂径定理得到弧BD=弧DC,即可得到结论;
(2)证明△ADC∽△CDE,由相似三角形的对应边成比例即可得到结论.
试题解析:解:(1)∵![]() 与⊙O相切于点P,∴PD⊥l.∵
与⊙O相切于点P,∴PD⊥l.∵ ![]() ∥BC,∴PD⊥BC,∴ PD平分弦BC ,∴弧BD=弧DC , ∴∠BAD=∠DAC ,即AD平分∠BAC;
∥BC,∴PD⊥BC,∴ PD平分弦BC ,∴弧BD=弧DC , ∴∠BAD=∠DAC ,即AD平分∠BAC;
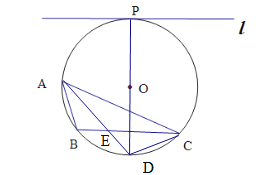
(2)∠BAD=∠BCD且∠BAD=∠DAC,∴ ∠DAC=∠BCD.
在△ADC和△CDE中
∵∠DAC=∠BCD,∠ADC=∠EDC,∴△ADC∽△CDE ,
∴![]() ,
, ![]() ,∴DC=4.
,∴DC=4.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目