题目内容
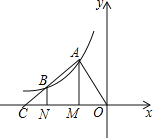
【题目】如图,点A、B在反比例函数y=![]() 的图象上,过点A、B作x轴的垂线,垂足分别是M、N,射线AB交x轴于点C,若OM=MN=NC,四边形AMNB的面积是3,则k的值为( )
的图象上,过点A、B作x轴的垂线,垂足分别是M、N,射线AB交x轴于点C,若OM=MN=NC,四边形AMNB的面积是3,则k的值为( )
A.2 B.4 C.﹣2 D.﹣4
【答案】D
【解析】
试题分析:根据三角形面积公式得到S△AOM=![]() S△AOC,S△ACM=4S△BCN,再根据反比例函数的比例系数k的几何意义得到S△AOM=
S△AOC,S△ACM=4S△BCN,再根据反比例函数的比例系数k的几何意义得到S△AOM=![]() |k|,然后利用k<0去绝对值求解.
|k|,然后利用k<0去绝对值求解.
解:∵点A、B在反比例函数y的图象上,
∴S△AOM=![]() |k|,
|k|,
∵OM=MN=NC,
∴AM=2BN,
∴S△AOM=![]() S△AOC,S△ACM=4S△BCN,S△ACM=2S△AOM,
S△AOC,S△ACM=4S△BCN,S△ACM=2S△AOM,
∵四边形AMNB的面积是3,
∴S△BCN=1,
∴S△AOM=2,
∴|k|=4,
∵反比例函数y=![]() 的图象在第二四象限,
的图象在第二四象限,
∴k=﹣4,
故选D.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目