Question

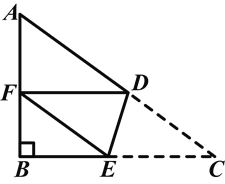
【题目】如图，在△ABC中，∠B＝90°，AB＝6，BC＝8，将△ABC沿DE折叠，使点C落在AB边上的点F处，并且FD∥BC，则CD的长是( )

A.

B.

C.

D.

Answer 1

【答案】A

【解析】试题分析：本题主要考查的是相似三角形的性质和判定、翻折的性质、勾股定理的应用，利用相似三角形的性质列出关于x的方程是解题的关键．先利用勾股定理求得AB的长，然后由翻折的性质可知DF=DB，由DF∥BC可知△AFD∽△ACB，利用相似三角形的性质列出方程求解即可．

解：在Rt△ABC中，由勾股定理得：AB===10．

由翻折的性质可知：DF=DB．

设BD=x，则DF=x．

∵DF∥BC，

∴△AFD∽△ACB．

∴＝，即＝．

解得：x=．

故选：A．