Question

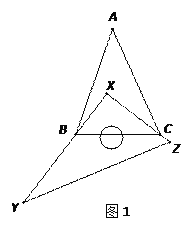
【题目】（1）如图1，有一块直角三角板XYZ（其中∠X=90°）放置在△ABC上，恰好三角板XYZ的两条直角边XY，XZ分别经过B，C两点，且直角顶点X在△ABC内部．

①若∠A=40°，∠ABC+∠ACB= °；∠XBC+∠XCB= °；

②试判断∠A与∠XBA+∠XCA之间存在怎样数量关系？并写出证明过程．

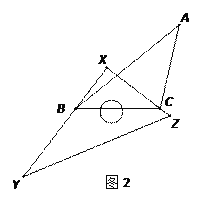
（2）如图2，如果直角顶点X在△ABC外部，试判断∠A、∠XBA、∠XCA之间又存在怎样的数量关系？（只写出答案，无需证明）．

Answer 1

【答案】（1）①140，90；②∠A+∠XBA+∠XCA=90°，证明见解析；（2）∠A+（∠XBA－∠XCA）=90°

【解析】试题分析：（1）①根据三角形内角和定理可得∠ABC+∠ACB=180°﹣∠A=140°，∠XBC+∠XCB=180°﹣∠XBC=90°，进而可求出∠ABX+∠ACX的度数；

②根据三角形内角和定义有90°+（∠ABX+∠ACX）+∠A=180°，则可得出结论．

（2）由②的解题思路可得：∠A+（∠XBA－∠XCA）=90°．

（1）①若∠A=40°，∠ABC+∠ACB= 140 °；

∠XBC+∠XCB= 90 °；

②∠A+∠XBA+∠XCA=90°（或等式的变形也可以）

证明：∵∠X=90°

∴∠XBC+∠XCB=180°－∠X=90°

∵∠A+∠ABC+∠ACB=180°，

∴∠A+（∠XBA+∠XCA）+（∠XBC+∠XCB）=180°，

∴∠A+（∠XBA+∠XCA）=180°－90°=90°，

∴∠A=90°－（∠XBA+∠XCA）

（2） ∠A+（∠XBA－∠XCA） =90°．