题目内容
【题目】已知
，
，
(
)．
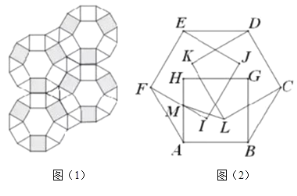
（1）观察猜想
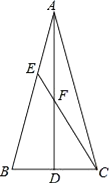
如图1，当
时，请直接写出线段
与
的数量关系： ；位置关系： ；
（2）类比探究
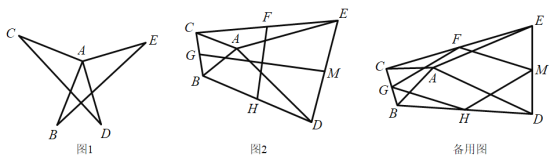
如图2，已知
，
分别是
，
，
，
的中点，写出
与
的数量关系和位置关系，并说明理由；
（3）解决问题
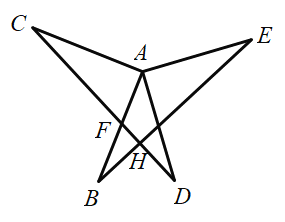
如图，已知：
，
，分别是，，，的中点，将
绕点
旋转，直接写出四边形
的面积
的范围(用含
的三角函数式子表示)．
【答案】（1）
，
；（2）
，
，理由见解析；（3）
．
【解析】
（1）利用三角形全等三角形或图形旋转的性质问题可解；
（2）在（1）中结论的基础上，利用三角形中位线的性质证明四边形
是菱形，证明，利用锐角三角函数的知识可证明；
（3）在（2）的基础上，证明四边形是菱形，利用中位线性质证明到菱形的边GF是CD的一半，通过旋转的过程得到CD的取值范围，再利用三角函数的知识，表示菱形面积，则问题可解．
（1）如图
∵
∴
∵
，
，
∴
∴
，
=
∵
∴
故答案为：，
（2），．
理由如下：
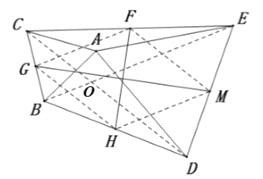
连接，，
交于
，
∵
，
∴
∵，，
∴
，
∴，
，
∴
，
连接
，
∵
分别是
的中点，
∴
，
，
，
，
，
，
∴
，
，
∴四边形是菱形，
∴
∵
，
∴．
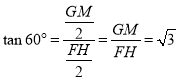（3）
如图，
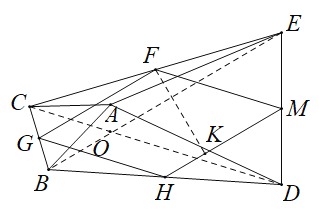
由（2）同理可知，四边形是菱形，
，
将
绕点
旋转过程中，
则菱形的边长GF范围为
过F做
于K
菱形的面积为
写出四边形的面积
的范围为：
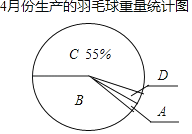
亮点激活精编提优100分大试卷系列答案
【题目】一只羽毛球的重量合格标准是5.0克～5.2克（含5.0克，不含5.2克），某厂对4月份生产的羽毛球重量进行抽样检验．并将所得数据绘制成如图统计图表．
4月份生产的羽毛球重量统计表
组别 | 重量x（克） | 数量（只） |
A | x＜5.0 | m |
B | 5.0≤x＜5.1 | 400 |
C | 5.1≤x＜5.2 | 550 |
D | x≥5.2 | 30 |
（1）求表中m的值及图中B组扇形的圆心角的度数．
（2）问这些抽样检验的羽毛球中，合格率是多少？如果购得4月份生产的羽毛球10筒（每筒12只），估计所购得的羽毛球中，非合格品的羽毛球有多少只？
