Question

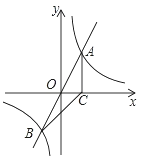
【题目】如图，正比例函数的图像与反比例函数的图像交于、两点，过点作垂直轴于点，连结.若的面积为2.

（1）求的值；

（2）直接写出：①点坐标____________；点坐标_____________；②当时，的取值范围__________________；

（3）轴上是否存在一点，使为直角三角形？若存在，求出点的坐标；若不存在，请说明理由.

Answer 1

【答案】（1）；（2）①，；②或；（3）存在，坐标为或，或.

【解析】

（1）首先根据反比例函数与正比例函数的图象特征，可知A、B两点关于原点对称，则O为线段AB的中点，故△BOC的面积等于△AOC的面积，都等于1，然后由反比例函数y=的比例系数k的几何意义，可知△AOC的面积等于 |k|，从而求出k的值；

（2）联立两函数即可求出坐标，根据图像可写出范围.

（3）设点坐标为连结、，再根据勾股定理解答即可.

解：（1）由题意知：点与点关于原点对称，点为中点，

所以

又

所以

所以

（2）已知两函数交于A，B两点，

故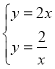

①点坐标，点坐标

②根据图像可得即是反比例函数在正比例函数下方的范围：或.

（3）设点坐标为连结、；　

∴

或

或

当或或时，

三角形为直角三角形，解得或或

所以点坐标为或，或