题目内容
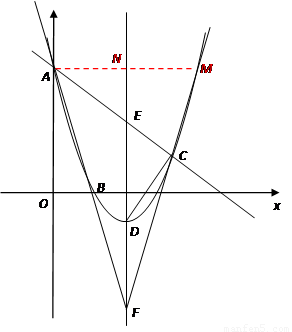
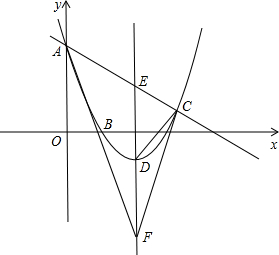 如图,已知抛物线过点A(0,6),B(2,0),C(7,
如图,已知抛物线过点A(0,6),B(2,0),C(7,| 5 | 2 |
(1)求抛物线的解析式;
(2)若D是抛物线的顶点,E是抛物线的对称轴与直线AC的交点,F与E关于D对称,求证:∠CFE=∠AFE;
(3)在y轴上是否存在这样的点P,使△AFP与△FDC相似?若有请求出所有符和条件的点P的坐标;若没有,请说明理由.
分析:(1)设抛物线解析式为y=ax2+bx+c,将A、B、C三点坐标代入,列方程组求抛物线解析式;
(2)求直线AC的解析式,确定E点坐标,根据对称性求F点坐标,分别求直线AF,CF的解析式,确定两直线与x轴的交点坐标,判断两个交点关于抛物线对称轴对称即可;
(3)存在.由∠CFE=∠AFE=∠FAP,△AFP与△FDC相似时,顶点A与顶点F对应,根据△AFP∽△FDC,△AFP∽△FCD,两种情况求P点坐标.
(2)求直线AC的解析式,确定E点坐标,根据对称性求F点坐标,分别求直线AF,CF的解析式,确定两直线与x轴的交点坐标,判断两个交点关于抛物线对称轴对称即可;
(3)存在.由∠CFE=∠AFE=∠FAP,△AFP与△FDC相似时,顶点A与顶点F对应,根据△AFP∽△FDC,△AFP∽△FCD,两种情况求P点坐标.
解答:(1)解:设抛物线解析式为y=ax2+bx+c,将A、B、C三点坐标代入,得
,
解得
,
∴抛物线解析式为y=
x2-4x+6;
(2)证明:设直线AC的解析式y=mx+n,
将A、C两点坐标代入,得
,
解得
,
∴y=-
x+6,
∵y=
x2-4x+6=
(x-4)2-2,
∴D(4,-2),E(4,4),
∵F与E关于D对称,
∴F(4,-8),则直线AF的解析式为y=-
x+6,CF的解析式为y=
x-22,
∴直线AF,CF与x轴的交点坐标分别为(
,0),(
,0),
∵4-
=
-4,
∴两个交点关于抛物线对称轴x=4对称,
∴∠CFE=∠AFE;
(3)解:存在.
设P(0,d),则AP=|6-d|,AF=
=2
,
FD=-2-(-8)=6,CF=
=
,
∵∠PAF=∠CFD,
∴点P位于点A的下方,
当△AFP∽△FDC时,
=
,即
=
,解得d=-
,
当△AFP∽△FCD时,
=
,即
=
,解得d=-2,
∴P点坐标为(0,-
)或(0,-2).
|
解得
|
∴抛物线解析式为y=
| 1 |
| 2 |
(2)证明:设直线AC的解析式y=mx+n,
将A、C两点坐标代入,得
|
解得
|
∴y=-
| 1 |
| 2 |
∵y=
| 1 |
| 2 |
| 1 |
| 2 |
∴D(4,-2),E(4,4),
∵F与E关于D对称,
∴F(4,-8),则直线AF的解析式为y=-
| 7 |
| 2 |
| 7 |
| 2 |
∴直线AF,CF与x轴的交点坐标分别为(
| 12 |
| 7 |
| 44 |
| 7 |
∵4-
| 12 |
| 7 |
| 44 |
| 7 |
∴两个交点关于抛物线对称轴x=4对称,
∴∠CFE=∠AFE;
(3)解:存在.
设P(0,d),则AP=|6-d|,AF=
| 42+(6+8)2 |
| 53 |
FD=-2-(-8)=6,CF=
(7-4)2+(
|
3
| ||
| 2 |
∵∠PAF=∠CFD,
∴点P位于点A的下方,
当△AFP∽△FDC时,
| AP |
| AF |
| FC |
| FD |
| 6-d | ||
2
|
| ||||
| 6 |
| 41 |
| 2 |
当△AFP∽△FCD时,
| AP |
| AF |
| FD |
| FC |
| 6-d | ||
2
|
| 6 | ||||
|
∴P点坐标为(0,-
| 41 |
| 2 |
点评:本题考查了二次函数的综合运用.关键是根据已知条件求抛物线解析式,根据抛物线的对称性,相似三角形的知识解题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
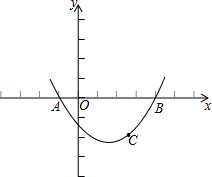 如图,已知抛物线过点A(-1,0)、B(4,0)、
如图,已知抛物线过点A(-1,0)、B(4,0)、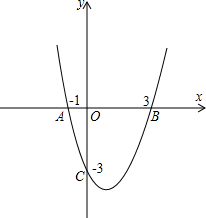 如图,已知抛物线过点A(-1,0)、B(3,0)、C(0,-3).
如图,已知抛物线过点A(-1,0)、B(3,0)、C(0,-3). 如图,已知抛物线过点A(0,6),B(2,0),C(6,0),直线AB交抛物线的对称轴于点F,直线AC交抛物线对称轴于点E.
如图,已知抛物线过点A(0,6),B(2,0),C(6,0),直线AB交抛物线的对称轴于点F,直线AC交抛物线对称轴于点E.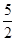 ). 若D是抛物线的顶点,E是抛物线的对称轴与直线AC的交点,F与E关于D对称.
). 若D是抛物线的顶点,E是抛物线的对称轴与直线AC的交点,F与E关于D对称.