题目内容
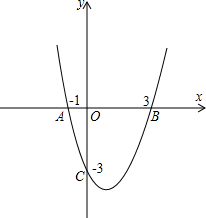 如图,已知抛物线过点A(-1,0)、B(3,0)、C(0,-3).
如图,已知抛物线过点A(-1,0)、B(3,0)、C(0,-3).(1)求该抛物线的解析式及其顶点的坐标;
(2)若P是抛物线上C、B两点之间的一动点,请连接CP、BP,是否存在点P,使得四边形OBPC的面积最大?若存在,求出点P的坐标;若不存在,请说明理由.
分析:(1)设出二次函数的一般形式后代入三个点的坐标求解即可;
(2)设存在点P(x,x2-2x-3),使得四边形OBPC的面积最大,作PD⊥x轴于点D,根据S四边形OCPB=S梯形OCPD+S△PBD得到有关x的最大值后即可求解
(2)设存在点P(x,x2-2x-3),使得四边形OBPC的面积最大,作PD⊥x轴于点D,根据S四边形OCPB=S梯形OCPD+S△PBD得到有关x的最大值后即可求解
解答: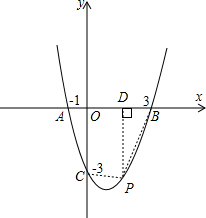 解:(1)设抛物线的解析式为y=ax2+bx+c,
解:(1)设抛物线的解析式为y=ax2+bx+c,
∵过点A(-1,0)、B(3,0)、C(0,-3),
∴
解得:
∴抛物线的解析式为:y=x2-2x-3
∵y=x2-2x-3=(x-1)2-4,
∴顶点坐标为(1,-4);
(2)设存在点P(x,x2-2x-3),使得四边形OBPC的面积最大,
如图,作PD⊥x轴于点D,
则OD=x,PD=-(x2-2x-3)=3+2x-x2,DB=3-x,
S四边形OCPB=S梯形OCPD+S△PBD=
(OC+PD)•OD+
DB•DP=
×(3+3+2x-x2)•x+
(3-x)(3+2x-x2)=-
(x-
)2+
则当x=
时,面积最大,
此时点P的坐标为:(
,-
).
 解:(1)设抛物线的解析式为y=ax2+bx+c,
解:(1)设抛物线的解析式为y=ax2+bx+c,∵过点A(-1,0)、B(3,0)、C(0,-3),
∴
|
解得:
|
∴抛物线的解析式为:y=x2-2x-3
∵y=x2-2x-3=(x-1)2-4,
∴顶点坐标为(1,-4);
(2)设存在点P(x,x2-2x-3),使得四边形OBPC的面积最大,
如图,作PD⊥x轴于点D,
则OD=x,PD=-(x2-2x-3)=3+2x-x2,DB=3-x,
S四边形OCPB=S梯形OCPD+S△PBD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 63 |
| 8 |
则当x=
| 3 |
| 2 |
此时点P的坐标为:(
| 3 |
| 2 |
| 15 |
| 4 |
点评:本题着重考查了待定系数法求二次函数解析式、四边形的面积等知识点,综合性强,考查学生数形结合的数学思想方法.

练习册系列答案
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
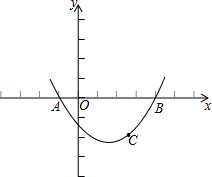 如图,已知抛物线过点A(-1,0)、B(4,0)、
如图,已知抛物线过点A(-1,0)、B(4,0)、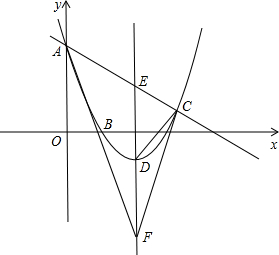 如图,已知抛物线过点A(0,6),B(2,0),C(7,
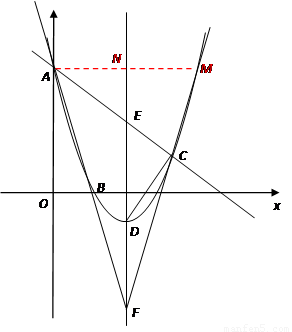
如图,已知抛物线过点A(0,6),B(2,0),C(7,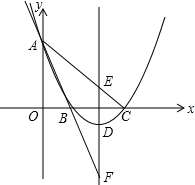 如图,已知抛物线过点A(0,6),B(2,0),C(6,0),直线AB交抛物线的对称轴于点F,直线AC交抛物线对称轴于点E.
如图,已知抛物线过点A(0,6),B(2,0),C(6,0),直线AB交抛物线的对称轴于点F,直线AC交抛物线对称轴于点E.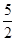 ). 若D是抛物线的顶点,E是抛物线的对称轴与直线AC的交点,F与E关于D对称.
). 若D是抛物线的顶点,E是抛物线的对称轴与直线AC的交点,F与E关于D对称.