题目内容
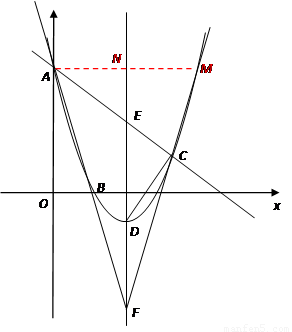
如图,已知抛物线过点A(0,6),B(2,0),C(7,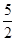 ). 若D是抛物线的顶点,E是抛物线的对称轴与直线AC的交点,F与E关于D对称.
). 若D是抛物线的顶点,E是抛物线的对称轴与直线AC的交点,F与E关于D对称.
(1)求抛物线的解析式;
(2)求证:∠CFE=∠AFE;
(3)在y轴上是否存在这样的点P,使△AFP与△FDC相似,若有,请求出所有合条件的点P的坐标;若没有,请说明理由.
解:(1)抛物线经过点A(0,6),B(2,0),C(7, )的抛物线的解析式为y=ax2+bx+c,
)的抛物线的解析式为y=ax2+bx+c,
则:
解得
∴ 此抛物线的解析式为 
(2)过点A作AM∥x轴,交FC于点M,交对称轴于点N.
∵抛物线的解析式 可变形为
可变形为
∴抛物线对称轴是直线x =4,顶点D的坐标为(4,-2).则AN=4.
设直线AC的解析式为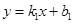 ,
,
则有 ,解得
,解得 .
.
∴ 直线AC的解析式为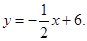
当x=4时,
∴点E的坐标为(4,4),
∵点F与E关于点D对称,则点F的坐标为(4,-8)
设直线FC的解析式为 ,
,
则有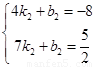 ,解得
,解得 .
.
∴ 直线AC的解析式为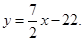
∵AM与x轴平行,则点M的纵坐标为6.
当y=6时,则有 解得x=8.
解得x=8.
∴AM=8,MN=AM—MN=4[来源:Zxxk.Com]
∴AN=MN
∵FN⊥AM
∴∠ANF=∠MNF
又NF=NF
∴△ANF≌△MNF
∴∠CFE=∠AFE
(3)∵C的坐标为(7, ),F坐标为(4,-8)
),F坐标为(4,-8)
∴
∵又A的坐标为(0,6),则 ,
,
又DF=6,
若△AFP∽△DEF
∵EF∥AO,则有∠PAF=∠AFE,
又由(2)可知∠DFC=∠AFE
∴∠PAF=∠DFC
若△AFP1∽△FCD
则 ,即
,即 ,解得P1A=8.
,解得P1A=8.
∴O P1=8-6=2
∴P1的坐标为(0,-2)
若△AFP2∽△FDC
则 ,即
,即 ,解得P2A=
,解得P2A=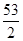 .
.
∴O P2=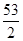 -6=
-6= .
.
∴P2的坐标为(0,- )
)
所以符合条件的点P的坐标不两个,分别是P1(0,-2),P2(0,- ).
).
【解析】(1)用待定系数法,知道抛物线上的三个点的坐标,可以用一般式来求解析式
(2)求证角相等,可以利用全等三角形或找中间量或放在等腰三角形里,本题通过构造两个全等的三角形来解决
(3)题目出现“使△AFP与△FDC相似”,肯定需要分情况讨论,由于∠PAF=∠DFC,
只有两种情况①△AFP∽△FCD②△AFP∽△FDC

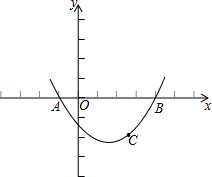 如图,已知抛物线过点A(-1,0)、B(4,0)、
如图,已知抛物线过点A(-1,0)、B(4,0)、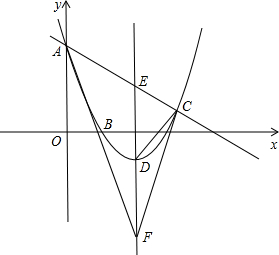 如图,已知抛物线过点A(0,6),B(2,0),C(7,
如图,已知抛物线过点A(0,6),B(2,0),C(7,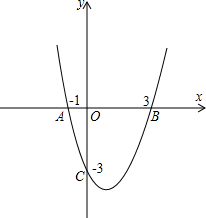 如图,已知抛物线过点A(-1,0)、B(3,0)、C(0,-3).
如图,已知抛物线过点A(-1,0)、B(3,0)、C(0,-3).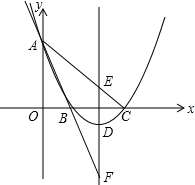 如图,已知抛物线过点A(0,6),B(2,0),C(6,0),直线AB交抛物线的对称轴于点F,直线AC交抛物线对称轴于点E.
如图,已知抛物线过点A(0,6),B(2,0),C(6,0),直线AB交抛物线的对称轴于点F,直线AC交抛物线对称轴于点E.