题目内容
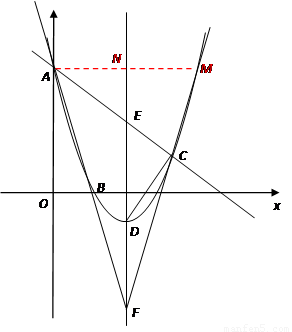
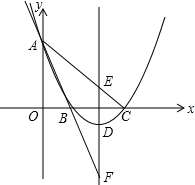 如图,已知抛物线过点A(0,6),B(2,0),C(6,0),直线AB交抛物线的对称轴于点F,直线AC交抛物线对称轴于点E.
如图,已知抛物线过点A(0,6),B(2,0),C(6,0),直线AB交抛物线的对称轴于点F,直线AC交抛物线对称轴于点E.(1)求抛物线的解析式;
(2)求证:点E与点F关于顶点D对称;
(3)在y轴上是否存在这样的点P,使△AFP与△FDC相似?若有,请求出所有合条件的点P的坐标;若没有,请说明理由.
分析:(1)根据点B、C的坐标设抛物线解析式为y=a(x-2)(x-6),把点A坐标代入求解得到a的值,即可得到函数解析式;
(2)根据抛物线解析式确定出对称轴与顶点坐标,利用待定系数法求出直线AB、AC的解析式,然后求出点E、F的坐标,即可得证;
(3)根据点A、B、C、D、F的坐标求出AF、FD、FC的长度,再利用正切函数确定出∠BAO=∠CFD,然后利用两边对应成比例,夹角相等,两三角形相似分两种情况列出比例式求出AP的长度,再求出OP的长度,即可得到点P的坐标.
(2)根据抛物线解析式确定出对称轴与顶点坐标,利用待定系数法求出直线AB、AC的解析式,然后求出点E、F的坐标,即可得证;
(3)根据点A、B、C、D、F的坐标求出AF、FD、FC的长度,再利用正切函数确定出∠BAO=∠CFD,然后利用两边对应成比例,夹角相等,两三角形相似分两种情况列出比例式求出AP的长度,再求出OP的长度,即可得到点P的坐标.
解答:解:(1)∵抛物线过点B(2,0),C(6,0),
∴设抛物线解析式为y=a(x-2)(x-6),
又∵抛物线经过点A(0,6),
∴a(0-2)(0-6)=6,
解得a=
,
所以,抛物线解析式为y=
(x-2)(x-6),
即y=
x2-4x+6;
(2)证明:∵y=
x2-4x+6=
(x2-8x+16)-2=
(x-4)2-2,
∴抛物线对称轴为直线x=4,顶点坐标为D(4,-2),
设直线AC解析式为y=kx+b,
则
,
解得
,
所以,直线AC的解析式为y=-x+6,
当x=4时,y=-4+6=2,
所以,点E(4,2),
所以,DE=2-(-2)=4,
设直线AB解析式为y=ex+f,
则
,
解得
,
所以,直线AB的解析式为y=-3x+6,
当x=4时,y=-3×4+6=-6,
所以,点F(4,-6),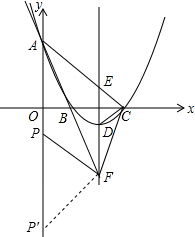
所以,DF=-2-(-6)=4,
所以,DE=DF,
故,点E与点F关于顶点D对称;
(3)解:∵A(0,6),B(2,0),C(6,0),D(4,-2),F(4,-6),
∴AF=
=4
,FD=-2-(-6)=4,FC=
=2
,
∵tan∠BAO=
=
=
,tan∠CFD=
=
,
∴∠BAO=∠CFD,
①当AP与FD是对应边时,∵△AFP∽△FCD,
∴
=
,
即
=
,
解得AP=8,
所以,OP=8-6=2,
此时,点P的坐标为(0,-2);
②当AP与FC是对应边时,∵△AFP∽△FDC,
∴
=
,
即
=
,
解得AP=20,
所以,OP=20-6=14,
此时,点P的坐标为(0,-14),
综上所述,存在点P(0,-2),(0,-14),使△AFP与△FDC相似.
∴设抛物线解析式为y=a(x-2)(x-6),
又∵抛物线经过点A(0,6),
∴a(0-2)(0-6)=6,
解得a=
| 1 |
| 2 |
所以,抛物线解析式为y=
| 1 |
| 2 |
即y=
| 1 |
| 2 |
(2)证明:∵y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴抛物线对称轴为直线x=4,顶点坐标为D(4,-2),
设直线AC解析式为y=kx+b,
则
|
解得
|
所以,直线AC的解析式为y=-x+6,
当x=4时,y=-4+6=2,
所以,点E(4,2),
所以,DE=2-(-2)=4,
设直线AB解析式为y=ex+f,
则
|
解得
|
所以,直线AB的解析式为y=-3x+6,
当x=4时,y=-3×4+6=-6,
所以,点F(4,-6),

所以,DF=-2-(-6)=4,
所以,DE=DF,
故,点E与点F关于顶点D对称;
(3)解:∵A(0,6),B(2,0),C(6,0),D(4,-2),F(4,-6),
∴AF=
| (6+6)2+42 |
| 10 |
| 62+(6-4)2 |
| 10 |
∵tan∠BAO=
| OB |
| OA |
| 2 |
| 6 |
| 1 |
| 3 |
| 6-4 |
| 6 |
| 1 |
| 3 |
∴∠BAO=∠CFD,
①当AP与FD是对应边时,∵△AFP∽△FCD,
∴
| AP |
| FD |
| AF |
| FC |
即
| AP |
| 4 |
4
| ||
2
|
解得AP=8,
所以,OP=8-6=2,
此时,点P的坐标为(0,-2);
②当AP与FC是对应边时,∵△AFP∽△FDC,
∴
| AP |
| FC |
| AF |
| FD |
即
| AP | ||
2
|
4
| ||
| 4 |
解得AP=20,
所以,OP=20-6=14,
此时,点P的坐标为(0,-14),
综上所述,存在点P(0,-2),(0,-14),使△AFP与△FDC相似.
点评:本题是二次函数综合题型,主要涉及待定系数法求函数解析式(包括二次函数解析式,直线解析式),两点间的距离公式,相似三角形对应边成比例的性质,(1)用交点式解析式求解比较简单,(3)先利用锐角的正切值相等判断出∠BAO=∠CFD是解题的关键.

练习册系列答案
相关题目
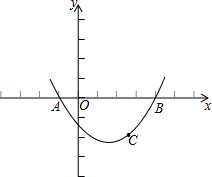 如图,已知抛物线过点A(-1,0)、B(4,0)、
如图,已知抛物线过点A(-1,0)、B(4,0)、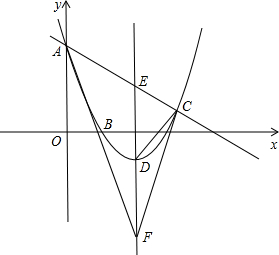 如图,已知抛物线过点A(0,6),B(2,0),C(7,
如图,已知抛物线过点A(0,6),B(2,0),C(7, 如图,已知抛物线过点A(-1,0)、B(3,0)、C(0,-3).
如图,已知抛物线过点A(-1,0)、B(3,0)、C(0,-3).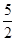 ). 若D是抛物线的顶点,E是抛物线的对称轴与直线AC的交点,F与E关于D对称.
). 若D是抛物线的顶点,E是抛物线的对称轴与直线AC的交点,F与E关于D对称.