题目内容
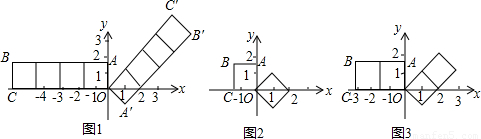
在平面直角坐标系xOy中,如图1,将若干个边长为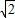 的正方形并排组成矩形OABC,相邻两边OA、OC分别落在y轴的正半轴和x轴的负半轴上,将这些正方形顺时针绕点O旋转135°得到相应矩形OA′B′C′,二次函数y=ax2+bx+c(a≠0)过点O、B′、C′.
的正方形并排组成矩形OABC,相邻两边OA、OC分别落在y轴的正半轴和x轴的负半轴上,将这些正方形顺时针绕点O旋转135°得到相应矩形OA′B′C′,二次函数y=ax2+bx+c(a≠0)过点O、B′、C′.(1)如图2,当正方形个数为1时,填空:点B′坐标为______,点C′坐标为______,二次函数的关系式为______,此时抛物线的对称轴方程为______;
(2)如图3,当正方形个数为2时,求y=ax2+bx+c(a≠0)图象的对称轴;
(3)当正方形个数为2011时,求y=ax2+bx+c(a≠0)图象的对称轴;
(4)当正方形个数为n个时,请直接写出:用含n的代数式来表示y=ax2+bx+c(a≠0)图象的对称轴.
【答案】分析:(1)根据正方形的性质求出对角线的长,然后根据旋转角是135°可知点C′在x轴上,从而求出点B′、C′的坐标,再利用待定系数法求二次函数解析式,根据对称轴公式求解;
(2)先求出点B′、C′的坐标,再利用待定系数法求出a、b的关系,然后利用对称轴解析式解答;
(3)求出点B′、C′的坐标,再利用待定系数法求出a、b的关系,然后利用对称轴解析式解答;
(4)根据(2)与(3)的规律,求出点B′、C′的坐标,再利用待定系数法求出a、b的关系,然后利用对称轴解析式解答即可.
解答:解:(1)∵正方形的边长为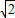 ,
,
∴对角线为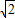 ×
×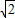 =2,
=2,
∵旋转角为135°,
∴点B′在x轴上,
∴点B′(2,0),
根据正方形的性质,点C′(1,1),
∵抛物线y=ax2+bx+c(a≠0)过点O、B′、C′,
∴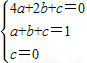 ,
,
解得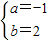 ,
,
∴二次函数关系式为y=-x2+2x,
对称轴为直线x=-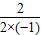 =1,
=1,
即直线x=1;
故答案为:(2,0);(1,1);y=-x2+2x;直线x=1.
(2)正方形个数为2时,B′(3,1),C′(2,2),
∴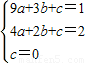 ,
,
整理得,7a=-2b,
∴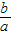 =-
=- ,
,
抛物线对称轴为直线x=-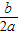 =-
=- ×(-
×(- )=
)= ;
;
(3)正方形个数为2011时,B′(2012,2010),C′(2011,2011),
∴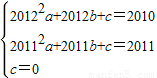 ,
,
整理得,6034a=-2b,
∴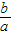 =-3017,
=-3017,
对称轴为直线x=-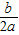 =-
=- ×(-3017)=
×(-3017)=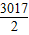 ;
;
(4)正方形个数为n个时,B′(n+1,n-1),C′(n,n),
∴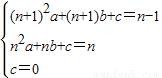 ,
,
整理得,(3n+1)a=-2b,
∴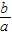 =-
=-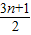 ,
,
对称轴为直线x=-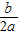 =-
=- ×(-
×(-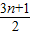 )=
)=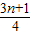 .
.
点评:本题是二次函数综合题型,主要考查了正方形的性质,旋转的性质,待定系数法的思想以及待定系数法求二次函数解析式,根据规律确定出点B′、C′的坐标是解题的关键,也是本题的难点.
(2)先求出点B′、C′的坐标,再利用待定系数法求出a、b的关系,然后利用对称轴解析式解答;
(3)求出点B′、C′的坐标,再利用待定系数法求出a、b的关系,然后利用对称轴解析式解答;
(4)根据(2)与(3)的规律,求出点B′、C′的坐标,再利用待定系数法求出a、b的关系,然后利用对称轴解析式解答即可.
解答:解:(1)∵正方形的边长为
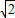 ,
,∴对角线为
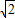 ×
×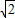 =2,
=2,∵旋转角为135°,
∴点B′在x轴上,
∴点B′(2,0),
根据正方形的性质,点C′(1,1),
∵抛物线y=ax2+bx+c(a≠0)过点O、B′、C′,
∴
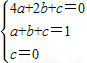 ,
,解得
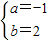 ,
,∴二次函数关系式为y=-x2+2x,
对称轴为直线x=-
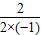 =1,
=1,即直线x=1;
故答案为:(2,0);(1,1);y=-x2+2x;直线x=1.
(2)正方形个数为2时,B′(3,1),C′(2,2),
∴
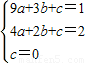 ,
,整理得,7a=-2b,
∴
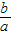 =-
=- ,
,抛物线对称轴为直线x=-
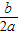 =-
=- ×(-
×(- )=
)= ;
;(3)正方形个数为2011时,B′(2012,2010),C′(2011,2011),
∴
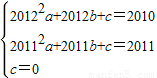 ,
,整理得,6034a=-2b,
∴
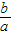 =-3017,
=-3017,对称轴为直线x=-
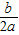 =-
=- ×(-3017)=
×(-3017)=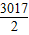 ;
;(4)正方形个数为n个时,B′(n+1,n-1),C′(n,n),
∴
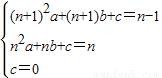 ,
,整理得,(3n+1)a=-2b,
∴
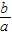 =-
=-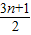 ,
,对称轴为直线x=-
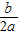 =-
=- ×(-
×(-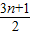 )=
)=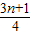 .
.点评:本题是二次函数综合题型,主要考查了正方形的性质,旋转的性质,待定系数法的思想以及待定系数法求二次函数解析式,根据规律确定出点B′、C′的坐标是解题的关键,也是本题的难点.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.
如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点. 如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为
如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为