Question

【题目】用一条直线截三角形的两边，若所截得的四边形对角互补，则称该直线为三角形第三条边上的逆平行线．如图1，DE为△ABC的截线，截得四边形BCED，若∠BDE+∠C=180°，则称DE为△ABC边BC的逆平行线．如图2，已知△ABC中，AB=AC，过边AB上的点D作DE∥BC交AC于点E，过点E作边AB的逆平行线EF，交边BC于点F．

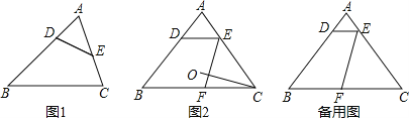
（1）求证：DE是边BC的逆平行线．

（2）点O是△ABC的外心，连接CO．求证：CO⊥FE．

（3）已知AB=5，BC=6，过点F作边AC的逆平行线FG，交边AB于点G．

①试探索AD为何值时，四边形AGFE的面积最大，并求出最大值；

②在①的条件下，比较AD+BG______AB大小关系．（“＜、＞或=”）

Answer 1

【答案】（1）见解析；（2）见解析；（3）①当AD=，四边形有最大值，最大值为，②=

【解析】

（1）根据题干条件可证得∠B=∠ACB，则∠BDE+∠B=180°，∠BDE+∠ACB=180°，结论得证；

（2）连接AO，证得∠FEC=∠B，由OA=OC可得∠OAC=∠OCA，∠BAO=∠OAC，证出∠FEC+∠ACB=90°，即CO⊥FE；

（3）①由题意设FC=x，则BF=6-x，证△FEC∽△ABC，可得，同理可得，四边形AGFE的面积可表示为S△ABC-S△EFC-S△BFG，利用二次函数的性质可求出最大值；

②由①知点F为BC的中点，连接DF，根据EF为AB边的逆平行线，可证得DF为AC边的逆平行线，则G点与D点重合，则AD+BG=AB．

解：（1）证明：

∵AB=AC，

∴∠B=∠ACB，

∵DE∥BC，

∴∠BDE+∠B=180°，∠BDE+∠ACB=180°，

∴DE是边BC的逆平行线．

（2）证明：如图，连接AO，

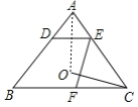
∵EF是边BA的逆平行线，

∴∠AEF+∠B=180°，

∵∠AEF+∠FEC=180°，

∴∠FEC=∠B，

∵点O是△ABC的外心，

∴OA=OC，OA平分∠BAC，

∴∠OAC=∠OCA，∠BAO=∠OAC，

∵∠BAO+∠B=90°，

∴∠FEC+∠ACB=90°，

∴CO⊥FE.

（3）①设FC=x，BF=6-x，S四边形AGFE=y，

∵∠FEC=∠B，∠FCE=∠ACB，

∴△FEC∽△ABC．

∴，

∴，

同理可得S△BFG=

∴y=S△ABC-S△EFC-S△BFG=12-=-，

∴当x=3时，有AD=，此时y有最大值，最大值为．

②在①的条件下CF=BF=3，如图，连接DF，

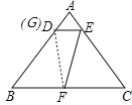
∵BF=CF，∠B=∠C，BD=CE，

∴△BDF≌△CEF（SAS），

∴∠BDF=∠CEF，∠BFD=∠EFC，

∴∠BFE=∠DFC，∠AEF=∠ADF．

∵∠AEF+∠B=180°，∠A+∠BFE=180°，

∴∠C+∠ADF=180°，∠A+∠DFC=180°．

∴FD为边AC的逆平行线，

由题意可知D与G点重合，

∴AD+BG=AB，

故答案为：=．