题目内容
【题目】如图所示,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°
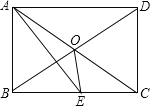
(1)求证:△ODC是等边三角形;
(2)求∠BOE
【答案】(1)证明见解析;(2)![]()
【解析】
(1)由矩形ABCD,得到OC=OD,根据AE平分∠BAD,∠BAE=∠DAE=45°=∠AEB,DEDAO AB=BE,因为∠CAE=15°,所以∠DAC=45°15°=30°,得出∠BAC=∠OCD=60°,即可证得△ODC是等边三角形.
(2)由等边三角形的性质,推出AB=OB,求出∠OAB、∠OBC的度数,根据平行线的性质和等角对等边得到OB=BE,根据三角形的内角和定理即可求出答案.
(1)∵四边形ABCD是矩形,
∴AD//BC,AC=BD,OA=OC,OB=OD,∠BAD=90°
∴OC=OD,∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE=45°=∠AEB,
∴AB=BE,
∵∠CAE=15°,
∴∠DAC=45°15°=30°,
∴∠BAC=∠OCD=60°
∴△ODC是等边三角形.
(2)∵OA=OB,∠BAC=∠OCD=60°
∵△AOB是等边三角形,
∴AB=OB,∠ABO=60°
∴∠OBC=90°60°=30°
∵AB=OB=BE,
∴∠BOE=∠BEO=![]() ×(180°30°)=75°
×(180°30°)=75°

【题目】小明同学以“你最喜欢的运动项目”为主题,对公园里参加运动的群众进行随机调查(每名被调查者只能选一个项目,且被调查者都进行了选择).下面是小明根据调查结果列出的统计表和绘制的扇形统计图(不完整).
被调查者男、女所选项目人数统计表
项目 | 男(人数) | 女(人数) |
广场舞 | 7 | 9 |
健步走 |
| 4 |
器械 | 2 | 2 |
跑步 | 5 |
|

根据以上信息回答下列问题:
(1)统计表中的![]() __________,
__________,![]() __________.
__________.
(2)扇形统计图中“广场舞”项目所对应扇形的圆心角度数为__________°.
(3)若平均每天来该公园运动的人数有3600人,请你估计这3600人中最喜欢的运动项目是“跑步”的约有多少人?
【题目】某小型企业实行工资与业绩挂钩制度,工人工资分为A、B、C、D四个档次.小明对该企业三月份工人工资进行调查,并根据收集到的数据,绘制了如下尚不完整的统计表与扇形统计图.
档次 | 工资(元) | 频数(人) | 频率 |
A | 3000 | 20 | |
B | 2800 | 0.30 | |
C | 2200 | ||
D | 2000 | 10 |
根据上面提供的信息,回答下列问题:
(1)求该企业共有多少人?
(2)请将统计表补充完整;
(3)扇形统计图中“C档次”的扇形所对的圆心角是 度.