题目内容
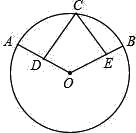
【题目】如图,C是以点O为圆心,AB为直径的半圆上一点,且CO⊥AB,在OC两侧分别作矩形OGHI和正方形ODEF,且点I,F在OC上,点H,E在半圆上,可证:IG=FD.小云发现连接图中已知点得到两条线段,便可证明IG=FD.
请回答:小云所作的两条线段分别是_____和_____;
证明IG=FD的依据是矩形的对角线相等,_____和等量代换.
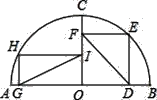
【答案】OH OE 同圆的半径相等
【解析】
连接OH、OE,由矩形OGHI和正方形ODEF的性质得出IG=OH,OE=FD,由OH=OE,即可得出结论.
解:
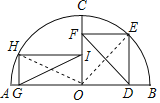
连接OH、OE,如图所示:
∵在矩形OGHI和正方形ODEF中,IG=OH,OE=FD,
∵OH=OE,
∴IG=FD;
故答案为:OH、OE,同圆的半径相等.

练习册系列答案
相关题目