题目内容
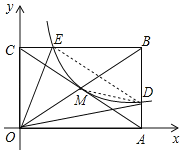
【题目】如图,反比例函数![]() 的图象经过矩形OABC的对角线的交点M,分别与AB、BC相交于点D、E,则下列结论正确的是______(填序号).
的图象经过矩形OABC的对角线的交点M,分别与AB、BC相交于点D、E,则下列结论正确的是______(填序号).
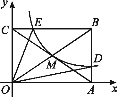
①![]() ;②连接MD,S△ODM=2S△OCE,;③
;②连接MD,S△ODM=2S△OCE,;③![]() ;④连接
;④连接![]() ,则△BED∽△BCA.
,则△BED∽△BCA.
【答案】①③④
【解析】
①正确.由四边形ABCD是矩形,推出S△OBC=S△OBA,由点E、点D在反比例函数y=![]() (x>0)的图象上,推出S△CEO=S△OAD=
(x>0)的图象上,推出S△CEO=S△OAD=![]() ,即可推出S△OEB=S△OBD.
,即可推出S△OEB=S△OBD.
②错误.因为![]() b=
b=![]() ab,所以S△ODM:S△OCE=
ab,所以S△ODM:S△OCE=![]() ,故错误.
,故错误.
③正确.设点B(m,n),D(m,n′)则M(![]() m,
m,![]() n,),由点M,点D在反比例函数y=
n,),由点M,点D在反比例函数y=![]() (x>0)的图象上,可得
(x>0)的图象上,可得![]() m
m![]() n=mn′,推出n′=
n=mn′,推出n′=![]() n,推出AD=
n,推出AD=![]() AB,推出BD=3AD,故正确.
AB,推出BD=3AD,故正确.
④正确.由![]() =3,推出DE∥AC,推出△BED∽△BCA.
=3,推出DE∥AC,推出△BED∽△BCA.
∵四边形ABCD是矩形,
∴S△OBC=S△OBA,
∵点E、点D在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴S△CEO=S△OAD=![]() ,
,
∴S△OEB=S△OBD,故①正确;
连接DM,∵S△ODM=S△OBD﹣S△BDM=![]() ,
,
∵S△CEO=S△OAD=![]() ,
,
∴S△ODM:S△OCE=![]() ,故②错误;
,故②错误;
设点B(m,n),D(m,n′)则M(![]() m,
m,![]() n,),
n,),
∵点M,点D在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴![]() m
m![]() n=mn′,
n=mn′,
∴n′=![]() n,
n,
∴AD=![]() AB,
AB,
∴BD=3AD,故③正确;
连接DE,同法可证CE=![]() BC,
BC,
∴BE=3EC,
∴![]() ,
,
∴DE∥AC,
∴△BED∽△BCA,故④正确.
故答案是:①③④.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目