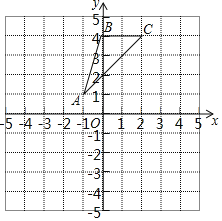题目内容
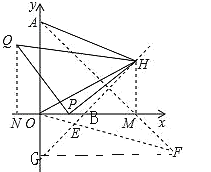
【题目】如图,在平面直角坐标系中,已知Q(﹣1,3),A(0,4),点P为x轴上一动点,以QP为腰作等腰Rt△QPH,当OH+AH最小时,点H的横坐标为_____.
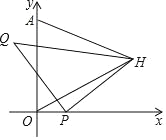
【答案】1.5
【解析】
作QN、HM垂直于x轴于N、M,则△QNP≌△PMH,推出PN=HM,QN=PM,设OP=x,得H(x+3,x+1),求出点H的运动轨迹即可解决问题.
解:作QN、HM垂直于x轴于N、M,
∵Rt△QPH是等腰三角形,
∴![]()
又![]()
∴![]()
∵QP=PH
∴△QNP≌△PMH,
∴PN=HM,QN=PM,设OP=x,得H(x+3,x+1),
∴H点在直线y=x-2上运动,
即H点在直线HG上运动,
作A点关于直线y=x-2的对称点F,
连OF交于点E,
当H点与E点重合时OH+AH最小,
令函数y=x-2,x=0,得y=-2, 令函数y=x-2=0,得x=2,
∴G(0,-2),B(2,0)
又k=1,
∴∠HBM=45°
可得∠AMN=45°,则∠FAG=45°
根据对称性可知AG=GF,
∴∠AFG=45°
故GF⊥AG
∴GF=6
则F(6,2)
设直线OF解析式为y=k2x
把F(6,2)代入得2=6k2,
∴k2=- ![]()
∴直线OF解析式为y=- ![]() x
x
联立函数y=x-2,解得x=1.5,y=0.5
∴E点的横坐标为1.5,
故答案为1.5.

练习册系列答案
相关题目