��Ŀ����
����Ŀ���Ķ����²��ϣ�������һ�����⣺����x��һԪ���η���ax2+bx+c��0��a��0������������ȵ��ҷ����ʵ������̽��a��b��c�����������
С������ѧϰ�����ľ��飬��Ϊ���ԴӶ��κ����ĽǶȿ�һԪ���η��̣�������С����̽�����̣�
����һԪ���η���ax2+bx+c��0��a��0����Ӧ�Ķ��κ���Ϊy��ax2+bx+c��a��0����
�ڽ������κ���ͼ���Եõ���Ӧ��һԪ������a��b��c������������б����£�
���̸��ļ������壺
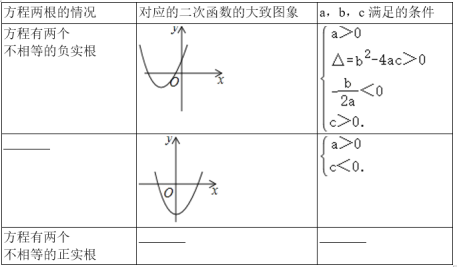
��1���ο�С��������������������������
��2����һԪ���η���mx2����2m+3��x��4m��0��һ����ʵ����һ����ʵ�����Ҹ�ʵ�����ک�1����ʵ��m��ȡֵ��Χ��
���𰸡���1������������������2��0��m��3
��������
��1���ɶ��κ�����һԪ���η��̵Ĺ�ϵ�Լ����κ�����ϵ���Ĺ�ϵ���ó��𰸣�
��2����m��0��m��0�������������������ͼ��ɵ�x=-1ʱy��ȡֵ��Χ���Ӷ��ó�����m�IJ���ʽ�飬�ⲻ��ʽ�鼴�ɣ�
��1����ȫ�������£�
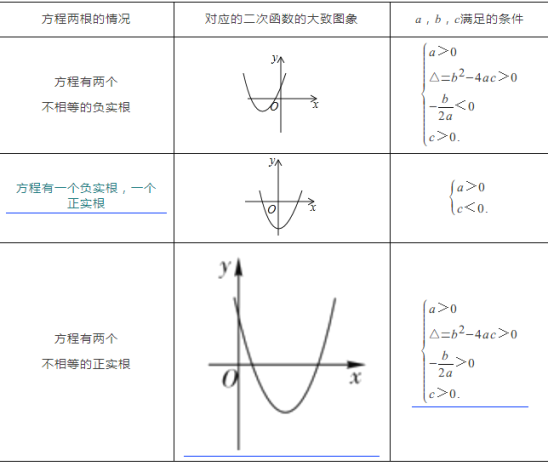
��2����һԪ���η���mx2����2m+3��x��4m��0��Ӧ�Ķ��κ���Ϊ��y��mx2����2m+3��x��4m��
��һԪ���η���mx2����2m+3��x��4m��0��һ����ʵ����һ����ʵ�����Ҹ�ʵ�����ک�1��
�ٵ�m��0ʱ��x����1ʱ��y��0��
��m+2m+3-4m��0
��ã�m��3��
��0��m��3��
�ڵ�m��0ʱ��x����1ʱ��y��0��
��m+2m+3-4m��0
��ã�m��3��������
��m��ȡֵ��Χ��0��m��3��