题目内容
【题目】如图,在△ABC中,∠B=90°,以AB为直径的⊙O交AC于D,过点D作⊙O的切线交BC于E,AE交⊙O于点F. 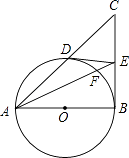
(1)求证:E是BC的中点;
(2)求证:ADAC=AEAF=4DO2 .
【答案】
(1)证明:连接BD,如下图所示,

∵AB是⊙O的直径,
∴BD⊥AC,
又∵∠ABC=90°,
∴CB切⊙O于点B,且ED且⊙O于点E,
∴EB=ED,
∴∠EBD=∠EDB,∠CDE+∠EDB=90°=∠EBD+∠C,
∴∠CDE=∠C,
∴ED=EC,
∴EB=EC,
即点E是BC的中点
(2)证明:∵AB=2OD,
∴AB2=4OD2,
连接BF,

由上图所示,
∵AB是⊙O的直径,
∴BF⊥AE,
∴△ABE∽△AFB,
∴ ![]() ,
,
∴AB2=AEAF,
同理可得,AB2=ADAC,
∴AB2=ADAC=AEAF,
即ADAC=AEAF=4DO2.
【解析】(1)要想证明E是BC的中点,只要证明CE=BE即可,根据已知条件可以得到DE=EC,DE=BE,从而本题得以解决;(2)根据题意可知AB=2OD,只要证明ADAC=AEAF=AB2即可,然后根据三角形相似可以证明结论成立,本题得以解决.
【考点精析】掌握切线的性质定理和相似三角形的判定与性质是解答本题的根本,需要知道切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
相关题目





